Алгоритми та їх властивості.

1) Неформальне поняття і визначення алгоритмів. Основні властивості алгоритмів.

2) Форми подання алгоритмів.

1) При вирішенні багатьох теоретичних та практичних задач необхідно визначити алгоритм, тобто такий набір інструкцій, виконуючи які ми за скінченну кількість кроків розв’яжемо поставлену задачу. Визначення точного поняття алгоритму є одним з найбільш значимих досягнень науки ХХ століття. Дане визначення було представлено в роботах Геделя, Черча, Поста, Т’юринга. Систематичне вивчення алгоритмів та моделей обчислення стало передумовою для створення ряду прикладних дисциплін.

В багатьох розділах математики, логіки та інформатики розглядаються процедури механічного характеру: в них необхідно знайти розв’язок конкретної задачі по даному правилу (алгоритму) для розв’язку задач певного класу.

Процедура алгоритму перетворює вхідні дані (Р) і направлена на отримання обумовленого цими даними результату (вихідний об’єкт Q) Дана процедура складається з окремих елементів (тактів) роботи алгоритму. Кожен крок полягає в зміні одного набору даних на інший. Перехід від попереднього кроку до наступного відбувається по наперед заданому скінченому набору інструкцій. Вище зазначені інструкції не повинні містити ніяких здогадок та ймовірних міркувань, як зі сторони людини, так і машини. Дані інструкції необхідні виконувати. Окремі стани розглядають як заключні, або цільові при яких процес обчислення закінчується. При цьому на основі деякої інструкції визначається, що необхідно вважати результатом обчислення. Розглянемо 3 варіанта протікання алгоритмічного процесу:

1) На деякому етапі виникає стан, яких розглядається як заключний або цільовий, при цьому відбувається зупинка обчислення і визначається результат Q.

2) Кожний поточний стан змін наступний до нескінченності, тобто процес обчислення ніколи не зупиниться.

3) При деякому стані виникає ситуація, коли процес обчислення переривається без видачі результату.

У випадку 3 не має переходу до наступного кроку і не має результату обчислень, тоді говорять, що відбувається безрезультатна зупинка. Вважається, що алгоритм А можна застосувати до вхідного набору даних Р, тоді і тільки тоді, коли виникає випадок 1, тобто процес обчислення закінчився і отримано результат обчислень Q.

Даний результат позначаємо А(Р). Зауваження: у випадках 2 і 3 результат А(Р) не існує.

Термін алгоритм походить від латинського перекладу арабського імені середньоазіатського вченого Аль-Хорезмі –Мухамеда Бен Муси.

Базові властивості алгоритму:

1) Дискретність алгоритму – процес перетворення вхідного набору даних в алгоритм процесу відбувається по кроках. Кожний крок є змінною одного набору даних іншим набором.

2) Детермінованість алгоритму – в алгоритмічному процесі відбувається перетворення Р на вході алгоритму в об’єкт Q на виході. При цьому всі кроки алгоритму А , величини проміжних обчислень та вихідний об’єкт Q однозначно обумовлені значенням пари (А,Р). Детермінованість алгоритму означає, що при повторному використанні (А,Р) на виході знову отримаємо об’єкт Q.

3) Масовість алгоритму – це вимога знайти єдиний алгоритм розв’язку не окремої задачі, а серії задач з деякого класу. Відокремлення задач класу відбувається при варіації (зміні) вхідних даних.

Для кожного алгоритму існує деяка потенційно нескінченна сукупність Х можливих вхідних даних. З цієї сукупності вибираємо об’єкт (Р), що поступає на вхід алгоритму.

Абстракції теорії алгоритмів

Вивчаючи алгоритмів ми дотримуємося деяких угод (абстракцій) теорії алгоритмів. Алгоритмічний процес при визначенні результату Q з вхідних даних Р здійснюється за декілька кроків, число кроків може бути настільки великим, що досягнення результату Q може бути практично неможливим, але в загальній теорії алгоритмів ми не враховуємо практичне здійснення і вважаємо можливим виконувати будь-яку скінченну кількість кроків. Абстракція потенційної реалізації алгоритмів передбачає, що ми можемо оперувати як завгодно великими об’єктами.

Під алгоритмом розуміють скінченну сукупність правил, дій, які розташовані в певному порядку для розв’язання всіх задач певного класу. Щоб побудувати алгоритм, необхідно дотримуватись певних умов:

1) вхідні та вихідні дані задаються у вигляді послідовності слів;

2) процес розв’язання задачі є процес перетворення вхідних даних у вихідні;

3) процес перетворення складається з сукупності елементарних операцій формального характеру;

4) припустима елементарна операція – це проста механічна дія, результат якої не залежить від виконавця;

5) послідовність припустимих операцій не залежить від конкретних вхідних даних;

6) порядок виконання припустимих операцій визначений однозначно;

7) сукупність припустимих операцій визначається типом даних.

Введемо поняття абстрактного алфавіту – це будь-яка скінченна сукупність об’єктів, які називаються символами або літерами алфавіту.

Символи не мають ніякого змісту. Слова в алфавіті – будь-яка скінченна впорядкована сукупність з його символів. Кількість символів у слові визначають його довжину. Якщо довжина слова дорівнює 0, то слово називається пустим.

Алфавітним оператором або відображенням 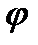називають будь-яку відповідність (функцію), яка зіставляє слова в тому самому або іншому алфавіті.

Якщо алфавітний оператор співставляє з вхідним словом лише одне вихідне, то він є однозначним. Саме такиі оператори використовується в алгоритмах, бо тільки вони забезпечують їм властивості алгоритму, тобто один єдиний результат як кожної операції, так і алгоритму в цілому.

Теорема: Існує теорема за якою кожному алфавітному оператору в алфавіті А відповідає алфавітний оператор в алфавіті В спряжений з ним.

Алфавітні оператори, що задаються за допомогою системи правил називають алгоритмами.

Таким чином, алгоритмом є алфавітний оператор разом із правилами, що встановлює його дії.

Два алфавітних оператори є рівні, якщо вони мають одну й ту саму область визначення і кожному слову з тієї області ставлять у відповідності ставлять однакові вихідні слова.

Два алгоритми є еквівалентними, якщо в них збігається алфавітні оператори, а способи їх задання (реалізація) не збігається.

Характеристики алгоритму:

1) Область визначення алгоритму – множина даних до яких алгоритм застосований, якщо алгоритм зупиняється без результату, то говорять про незастосовність алгоритму до цих вхідних даних.

2) Складність алгоритму – величина, що характеризує довжину опису алгоритму.

3) Під алгоритмічним розв’язком масової проблеми розуміють можливість побудови алгоритму розв’язку всіх задач цього класу.

Форми та способи завдання алгоритму

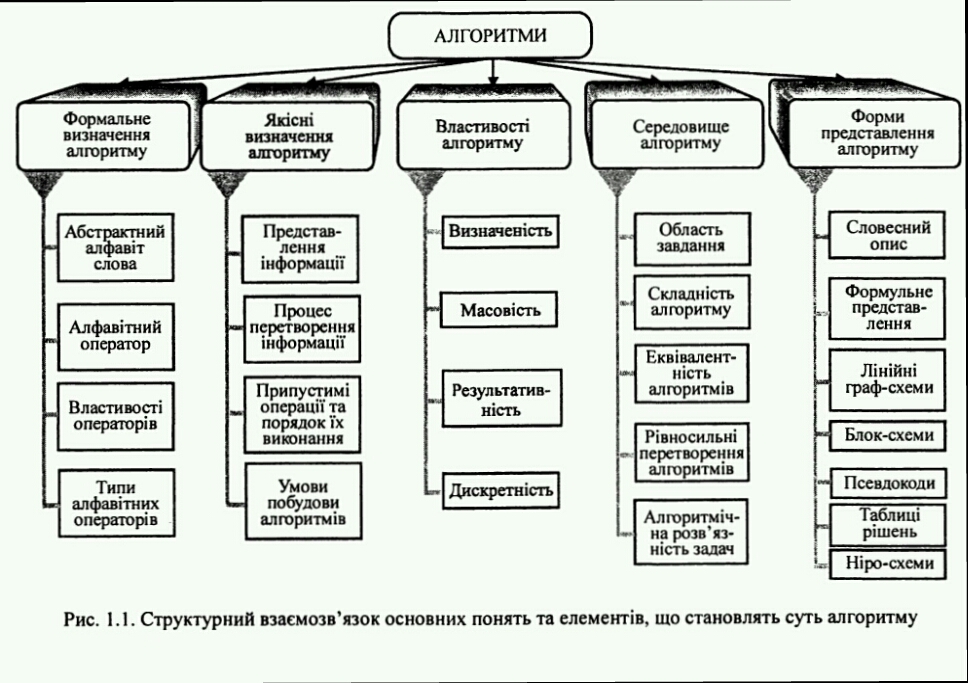
Існує різні форми представлення алгоритму:

1) Словесна

2) Словесно-формульна

3) Граф- схеми

4) Структурні схеми

5) Псевдокоди

6) НІРО-схеми

7) Таблиці рішень