Обчислювальні за Т’юрингом функції.
Визначення: Функція називається обчислювальною за Т’юрингом, якщо існує машина Т’юринга, що обчислює її значення для тих наборів значень аргументів, для яких функція визначена і працює нескінченно довго, якщо функція для даного набору значень аргументів невизначена.
Зауваження. 1.Розглядаємо функції, що задаються на множині натуральних чисел, і що приймають значення з множини натуральних чисел.
2. Значення 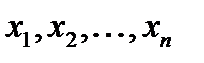 аргументів функції
аргументів функції 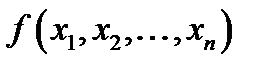 будемо розміщувати на стрічці у вигляді наступного слова:
будемо розміщувати на стрічці у вигляді наступного слова:
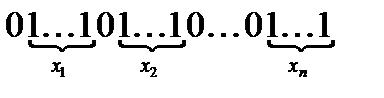
Введемо позначення
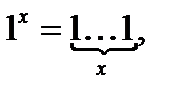
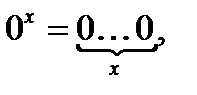
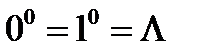 - пусте слово.
- пусте слово.
3. Переробку вхідного слова будемо починати зі стандартного положення, при якому в стані 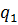 буде оглядатись крайня одиниця записаного слова, що розміщена праворуч. Якщо функція
буде оглядатись крайня одиниця записаного слова, що розміщена праворуч. Якщо функція 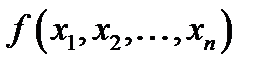 визначена на деякому наборі значень аргументів, то в результаті роботи машини Т’юринга на стрічці повинно бути записано послідовно
визначена на деякому наборі значень аргументів, то в результаті роботи машини Т’юринга на стрічці повинно бути записано послідовно 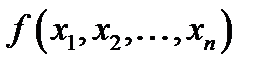 одиниць.
одиниць.
В іншому випадку машина Т’юринга повинна працювати нескінченно довго. При виконанні всіх перерахованих вище умов будемо говорити, що машина Т’юринга обчислює дану функцію. Побудова машини Т’юринга відбувається в 2 етапи:
1) Створюється алгоритм обчислення функції.
2) Алгоритм записується на мові машини Т’юринга.
Приклад 5.
Побудуємо машину Т’юринга, що обчислює функцію 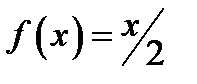 . Дана функція визначена не на всій множині натуральних чисел. Областю її визначення є множина всіх парних чисел. Тому необхідно побудувати таку машину Т’юринга, яка у випадку, коли на її вхід поступає парне число в якості результату отримувала б половину даного числа, а коли на її вхід поступає непарне число, працювала б необмежено довго. В якості зовнішнього алфавіту візьмемо двоелементну множину
. Дана функція визначена не на всій множині натуральних чисел. Областю її визначення є множина всіх парних чисел. Тому необхідно побудувати таку машину Т’юринга, яка у випадку, коли на її вхід поступає парне число в якості результату отримувала б половину даного числа, а коли на її вхід поступає непарне число, працювала б необмежено довго. В якості зовнішнього алфавіту візьмемо двоелементну множину 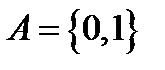 . В цьому алфавіті натуральне число
. В цьому алфавіті натуральне число 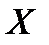 зображується словом 1…1, що складається з
зображується словом 1…1, що складається з 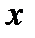 одиниць, що розміщені у комірках послідовно. Робота машини починається із стандартного початкового положення:
одиниць, що розміщені у комірках послідовно. Робота машини починається із стандартного початкового положення: 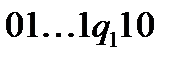 .
.
А) Розробимо комплекс команд, які забезпечують рух каретки машини Т’юринга ліворуч, при цьому кожну другу одиницю замінюємо на 0. Вищезазначену процедуру забезпечують наступні команди:
(1) 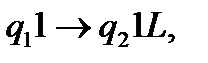
(2) 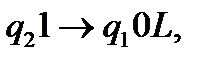
(3) 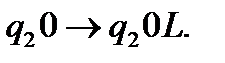
Якщо кількість одиниць непарна, то машина продовжує рух по стрічці необмежено ліворуч, тобто буде працювати нескінченно. Якщо число 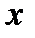 одиниць парне, то в результаті роботи машини Т’юринга утворюється конфігурація
одиниць парне, то в результаті роботи машини Т’юринга утворюється конфігурація 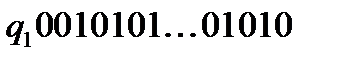 , в якій число одиниць дорівнює
, в якій число одиниць дорівнює 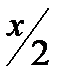 .
.
Б) Далі необхідно перемістити одиниці так, щоб між ними не стояли нулі.
Перемістимо каретку за першу одиницю, не змінюючи інформацію на стрічці.
(4) 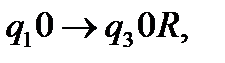
(5) 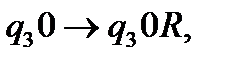
(6) 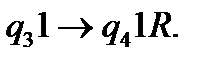
В результаті виконання команд (4)-(6) отримаємо конфігурацію: 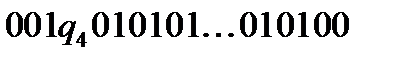 (*).
(*).
Замінимо 0, перед яким зупинилась каретка на 1 і перемістимося праворур до найближчого 0.
(7) 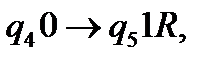
(8) 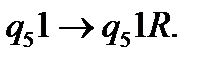
Отримаємо конфігурацію: 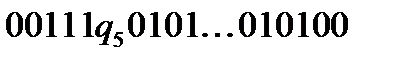 , в якій праворуч від комірки, яка переглядається записані пари 01,01,…,01. Крім того, на стрічці одна 1 записана зайва. Перемістимося по стрічці праворуч до останньої пари 01.
, в якій праворуч від комірки, яка переглядається записані пари 01,01,…,01. Крім того, на стрічці одна 1 записана зайва. Перемістимося по стрічці праворуч до останньої пари 01.
(9) 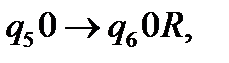
(10) 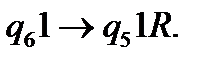
Отримаємо конфігурацію: 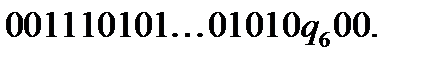
Повернемося на дві комірки назад і замінимо одиницю з останньої пари 01 на 0.
(11) 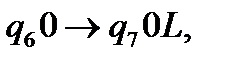
(12) 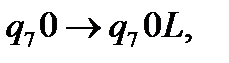
(13) 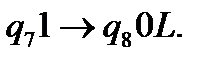
Отримаємо конфігурацію: 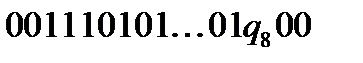 . Число одиниць на стрічці дорівнює
. Число одиниць на стрічці дорівнює 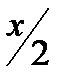 . Перемістимося ліворуч на одну комірку.
. Перемістимося ліворуч на одну комірку.
(14) 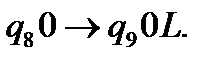
В результаті отримаємо конфігурацію: 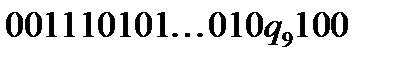 . Тепер замінимо праву одиницю на 0 і перемістимося по стрічці до наступної одиниці.
. Тепер замінимо праву одиницю на 0 і перемістимося по стрічці до наступної одиниці.
(15) 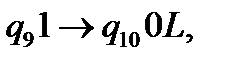
(16) 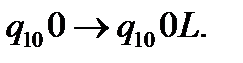
Тепер на стрічці не вистачає однієї одиниці (число одиниць дорівнює 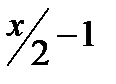 ).
).
Перемістимося по стрічці ліворуч до останньої пари 10.
(17) 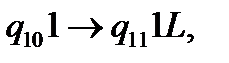
(18) 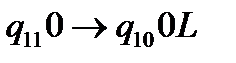 .
.
Послідовне виконання команд (17), (18) приведе до наступної конфігурації: 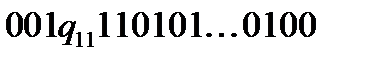 . Вернемося праворуч до найближчого нуля і замінимо його на 1.
. Вернемося праворуч до найближчого нуля і замінимо його на 1.
(19) 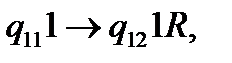
(20) 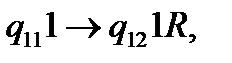
(21) 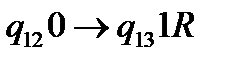 .
.
Отримаємо конфігурацію: 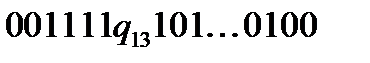 . В якій число одиниць знову дорівнює
. В якій число одиниць знову дорівнює 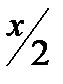 .
.
Якщо тепер перемістити каретку праворуч і перевести машину в стан 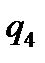 за допомогою команди
за допомогою команди 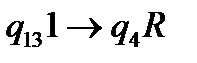 , то отримаємо конфігурацію:
, то отримаємо конфігурацію: 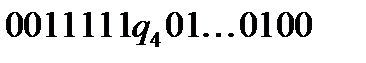 , яка аналогічна конфігурації (*).
, яка аналогічна конфігурації (*).
В результаті програма стає циклічною, знову найближчий нуль перетворюється в одиницю, а остання одиниця, що розміщується на стрічці праворуч, перетворюється в нуль. Потім машина переміщує каретку до першого нуля, що розміщується у слові ліворуч і т.д.
В деякий момент роботи програми конфігурація буде мати вигляд: 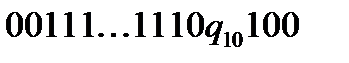 . Виконавши команди (17) і (18), отримаємо конфігурацію:
. Виконавши команди (17) і (18), отримаємо конфігурацію: 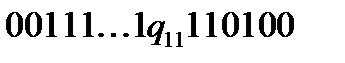 . В подальшому виконуються команди (19),(20),(21), що приводять до конфігурації
. В подальшому виконуються команди (19),(20),(21), що приводять до конфігурації 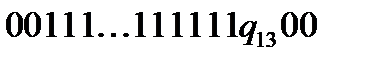 . Зупинимо машину за допомогою команди
. Зупинимо машину за допомогою команди 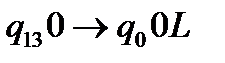 . Заключна конфігурація має вигляд:
. Заключна конфігурація має вигляд: 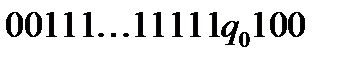 .
.
Таблична форма програми машини Т’юринга має вигляд:
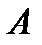
| |||
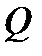
| |||
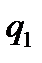
| 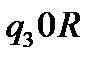
| 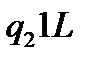
| |
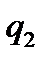
| 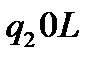
| 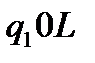
| |
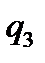
| 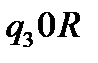
| 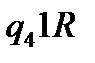
| |
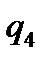
| 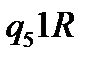
| ||
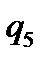
| 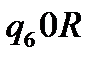
| 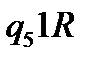
| |
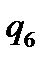
| 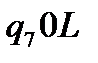
| 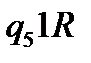
| |
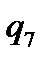
| 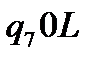
| 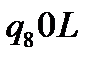
| |
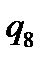
| 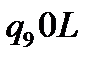
| 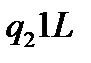
| |
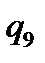
| 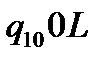
| ||
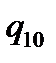
| 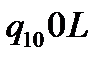
| 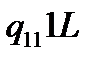
| |
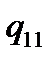
| 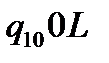
| 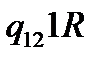
| |
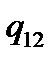
| 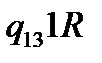
| 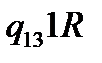
| |
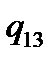
| 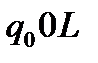
| 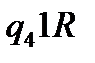
|
Дата добавления: 2015-10-13; просмотров: 1467;
