Правильна обчислювальність функцій за Т’юрингом.
Визначення. Будемо говорити, що машина Т’юринга правильно обчислює функцію 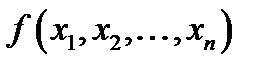 , якщо початкове слово
, якщо початкове слово 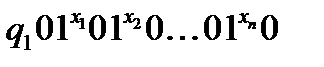 вона переводить у слово
вона переводить у слово 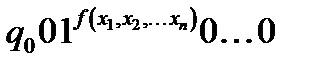 і при цьому не добудовує в процесі роботи на стрічці нових комірок ні ліворуч ні праворуч.
і при цьому не добудовує в процесі роботи на стрічці нових комірок ні ліворуч ні праворуч.
Якщо функція f не визначена на даному наборі значень аргументів, то, почавши роботу з указаного положення, машина Тюринга в процесі роботи не буде добудовувати комірки стрічки ліворуч.
Приклад 6.
Записати програми машини Т’юринга, що правильно обчислює функції
а) 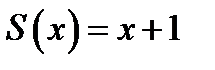 ,
,
б) 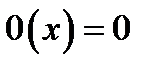 .
.
Розв’язання. а) Функція 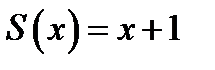 здійснює перехід
здійснює перехід 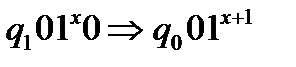 за допомогою команд:
за допомогою команд:
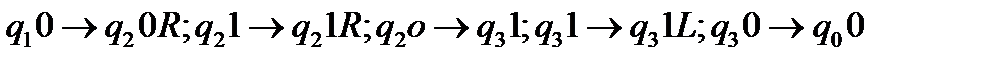 .
.
б) Функція 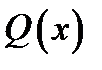 здійснює перехід
здійснює перехід 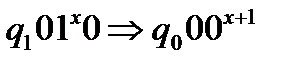 за допомогою команд
за допомогою команд
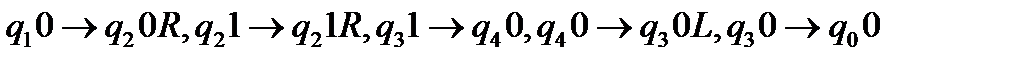 .
.
Відповідну машину Т’юринга назвали О.
Приклад 7.
Побудувати машину Т’юринга 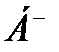 (зміщення ліворуч) та
(зміщення ліворуч) та 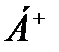 (зміщення праворуч).
(зміщення праворуч).
Перша з стандартного початкового положення перебудовує вхідне слово в те саме слово і зупиняється, оглядаючи крайню ліву комірку з нулем за допомогою команд: 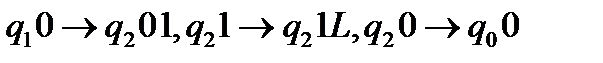 .
.
Програму машини 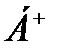 можна отримати з програми машини
можна отримати з програми машини 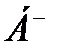 шляхом заміни символа “
шляхом заміни символа “ 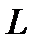 ” на символ “
” на символ “ 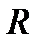 ”. Існує програма, яку називають транспозицією (позначають
”. Існує програма, яку називають транспозицією (позначають 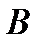 ), що дозволяє здійснити перехід
), що дозволяє здійснити перехід 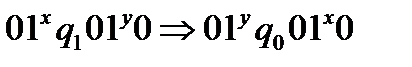 .
.
Композиція машин Т’юринга.
Нехай задані машини Т’юринга 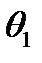 і
і 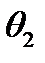 , що мають загальний зовнішній алфавіт
, що мають загальний зовнішній алфавіт 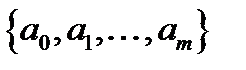 і алфавіти внутрішніх станів
і алфавіти внутрішніх станів 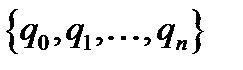 та
та 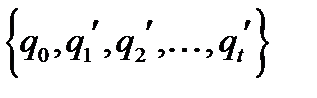 . Композицією машин (або добутком машини
. Композицією машин (або добутком машини 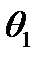 на
на 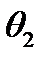 )
) 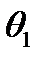 та
та 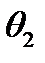 називається нова машина
називається нова машина 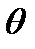 з тим самим зовнішнім алфавітом
з тим самим зовнішнім алфавітом 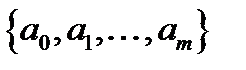 і внутрішнім алфавітом
і внутрішнім алфавітом 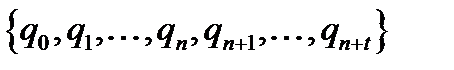 та програмою, що отримуємо наступним чином: у всіх командах із
та програмою, що отримуємо наступним чином: у всіх командах із 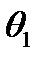 , що містять символ зупинки
, що містять символ зупинки 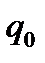 заміняємо його на
заміняємо його на 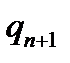 . Всі інші символи в командах з
. Всі інші символи в командах з 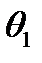 залишаються незмінними. В командах з
залишаються незмінними. В командах з 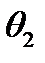 символ
символ 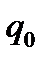 залишається незмінним, а всі інші стани
залишається незмінним, а всі інші стани 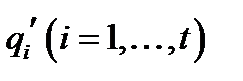 заміняємо відповідно на
заміняємо відповідно на 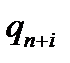 . Сукупність всіх команд, що отримані за вищезазначеними правилами утворює програму машини композиції
. Сукупність всіх команд, що отримані за вищезазначеними правилами утворює програму машини композиції 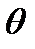 .
.
Поняття композиції є зручним інструментом для конструювання машин Т’юринга.
Дата добавления: 2015-10-13; просмотров: 1266;
