Конструювання машини.
Написання програми для машини це задача більш складна у порівнянні з задачею застосування машини до відповідних слів.
Приклад 4.
Побудувати машину Т’юринга яка з n одиниць, що записані на стрічці послідовно, залишить на стрічці n-2 одиниці, також записаних послідовно і працює нескінченно довго, якщо n=0 або n=1; F(x)=x-2
В якості зовнішнього алфавіту визначимо A= {0, 1}, де 0 –символ пустої комірки. Кількість необхідних внутрішніх станів будемо визначати в процесі побудови програми. Вважаємо, що машина починає працювати зі стандартного положення.
Машина в стані 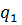 оглядає крайню одиницю з n записаних на стрічці, що записані праворуч. Зітремо першу одиницю, якщо вона існує, перейдемо до огляду наступної лівої комірки. Зітремо там одиницю, якщо вона в цій комірці записана. На кожному такому переході машина повинна переходити до нового стану (в протилежному випадку будуть знищені всі одиниці, що записані послідовно).
оглядає крайню одиницю з n записаних на стрічці, що записані праворуч. Зітремо першу одиницю, якщо вона існує, перейдемо до огляду наступної лівої комірки. Зітремо там одиницю, якщо вона в цій комірці записана. На кожному такому переході машина повинна переходити до нового стану (в протилежному випадку будуть знищені всі одиниці, що записані послідовно).
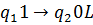
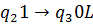
Машина знаходиться в стані 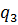 і оглядає третю праву комірку з тих, в яких записане дане слово, що складається з n одиниць. Не змінюючи змісту комірок машина повинна перейти до стану
і оглядає третю праву комірку з тих, в яких записане дане слово, що складається з n одиниць. Не змінюючи змісту комірок машина повинна перейти до стану 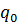 , не залежно від змісту комірки.
, не залежно від змісту комірки.
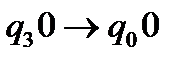
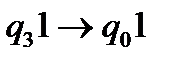 .
.
Розглянемо ситуації, коли на стрічці записана одна одиниця, або не записано жодної. Якщо записана на стрічці одна одиниця, то в стані 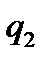 машина оглядає справа другу комірку, в якій записано 0. За умовою, машина повинна працювати вічно
машина оглядає справа другу комірку, в якій записано 0. За умовою, машина повинна працювати вічно
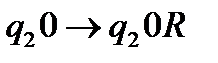 .
.
Аналогічно. Якщо на стрічці записаних одиниць не існує, то в початковому стані машина оглядає комірку з наповненням 0.
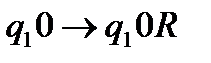 .
.
Дані команди заставляють рухатись машину необмежено праворуч.
Функціональну схему машини Т’юринга, що побудована за умовою приклада 4 можна подати у вигляді таблиці:
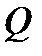
| 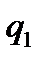
| 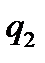
| 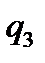
| |
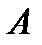
| ||||
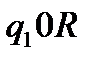
| 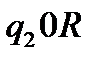
| 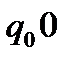
| ||
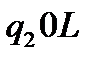
| 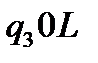
| 
|
Дата добавления: 2015-10-13; просмотров: 1383;
