Апроксимація функцій
Розглянемо застосування НМ як апарата для апроксимації функцій або побудови лінійних реґресійних моделей за експериментальними даними.
Як приклад створимо узагальнено-реґресійну НМ з ім'ям netдля апроксимації функції виду y=х2 на відрізку [-1, 1], використовуючи наступні експериментальні дані:
| x | -1 | -0.8 | -0.5 | -0.2 | 0.1 | 0.3 | 0.6 | 0.9 | ||
| y | 0.64 | 0.25 | 0.04 | 0.01 | 0.09 | 0.36 | 0.81 |
Процедура створення й використання даного типу НМ описується в такий спосіб:
» % Задання вхідних значень
» Р = [-1 -0.8 -0.5 -0.2 0 0.1 0.3 0.6 0.9 1];
» % Задання вихідних значень
» Т = [1 0.64 0.25 0.04 0 0.01 0.09 0.36 0.81 1];
» net = newgrnn(P,T,0.01); % Створення мережі із відхиленням 0.01
» Y = sim(net,[-0.9 -0.7 -0.3 0.4 0.8]) % Опитування мережі
Y =
0.8200 0.6400 0.0400 0.0900 0.8100
У даному випадку точність апроксимації є не дуже високою. Можна спробувати поліпшити якість апроксимації за рахунок підбору величини відхилення, але в умовах прикладу прийнятного результату легко досягти при використанні мережі з радіальними базисними елементами, «класичної» багатошарової або каскадної НМ із зворотним поширенням похибки. Створення й використання мережі з радіальними базисними елементами виконується наступним чином:
» net = newrbe(P,T);
» Y = sim(net,[-0.9 -0.7 -0.3 0.4 0.8]) % Опитування НМ
Y =
0.8100 0.4900 0.0900 0.1600 0.6400
Процедура створення, навчання й використання «класичної» багатошарової мережі відбувається у командному рядку наступним чином:
» net = newff([-1 1],[5 1],{'tansig' 'purelin'},'trainbr'); % Створення нової НМ
» net.trainParam.epochs = 50; % Задання кількості циклів навчання
» [net tr] = train(net,P,T); % Навчання мережі
TRAINBR, Epoch 0/50, SSE 26.7652/0, SSW 369.188, Grad 2.57e+001/1.00e-010, #Par 1.60e+001/16
TRAINBR, Epoch 25/50, SSE 1.15198e-005/0, SSW 25.854, Grad 1.05e-003/1.00e-010, #Par 7.91e+000/16
TRAINBR, Epoch 50/50, SSE 2.36514e-007/0, SSW 29.4473, Grad 7.39e-005/1.00e-010, #Par 8.88e+000/16
TRAINBR, Maximum epoch reached.
» Y = sim(net,[-0.9 -0.7 -0.3 0.4 0.8]) % Використання мережі
Y =
0.8107 0.4895 0.0904 0.1604 0.6397
» Y = sim(net,P);
» plot(P,T,P,Y,'о') % Графічна ілюстрація роботи мережі
Процес створення, навчання й використання каскадної мережі відбувається за допомогою наступних команд:
» net = newcf([-1 1],[5 1],{'tansig' 'purelin'});
» net.trainParam.epochs = 50;
» [net tr] = train(net,P,T);
TRAINLM. Epoch 0/50, MSE 7.77493/0. Gradient 138.282/le-010
TRAINLM. Epoch 25/50, MSE 4.01014e-010/0, Gradient 0.00028557/le-010
TRAINLM. Epoch 50/50. MSE 1.13636e-011/0, Gradient 1.76513e-006/le-010
TRAINLM, Maximum epoch reached, performance goal was not met.
» Y = sim(net,[-0.9 -0.7 -0.3 0.4 0.8])
Y =
0.7363 0.5898 0.0469 0.1478 0.6462
» Y = sim(net,P);
» plot(P,T,P,Y,'о');
Результати апроксимації з використанням різних НМ наведені на рис. 6.9.
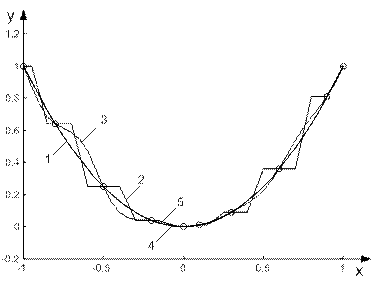
Рисунок 6.9 - Результати апроксимації функції y=x2 різними видами НМ:
1 - аналітичний розв’язок; 2, 3, 4, 5 - результат апроксимації з використанням узагальнено-реґресійної, каскадної, «класичної» багатошарової мереж і мережі з радіальними базисними елементами відповідно
На рис. 6.10 і 6.11 наведені графіки помилки апроксимації при використанні вищевказаних видів НМ та графіки зміни параметрів якості навчання «класичної» багатошарової НМ відповідно.
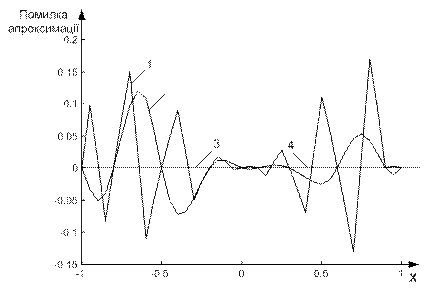
Рисунок 6.10 - Помилка апроксимації функції y=x2 різними видами НМ:
1, 2, 3, 4 - результат навчання узагальнено-реґресійної, каскадної, «класичної» багатошарової мереж і мережі з радіальними базисними елементами відповідно
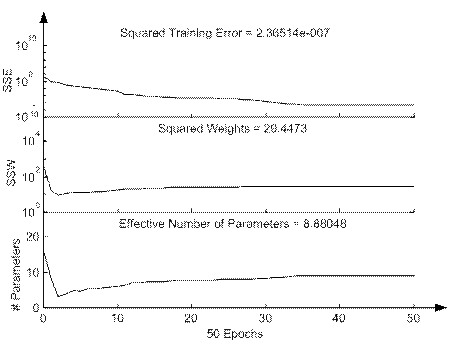
Рисунок 6.11 - Графіки зміни критеріїв якості «класичної» багатошарової мережі в процесі навчання
Розглянемо аналогічне завдання, але з використанням лінійної НМ мережі. Нехай експериментальні дані задані наступними значеннями:
| x | 1.0 | 1.5 | 3.0 | -1.2 |
| y | 1.5 | 3.0 | 1.0 |
Процес створення, навчання й використання лінійної НМ з ім'ям net ілюструється наведеним нижче лістингом і рис. 6.12, 6.13.
» Р = [1.0 1.5 3.0 -1.2];
» Т = [0.5 1.1 3.0 -1.0];
» % Визначення величини коефіцієнта навчання
» maxlr = maxlinlr(P,'bias');
» net = newlin([-2 2],1,[0],maxlr); % Створення лінійної мережі з ім'ям net
» net.tгаinParam.epochs = 15; % Задання кількості циклів навчання
» [net tr] = train(net,P,T) % Навчання мережі
TRAINWB. Epoch 0/15. MSE 2.865/0.
TRAINWB. Epoch 15/15. MSE 0.0730734/0.
TRAINWB. Maximum epoch reached.
» Y = sim(net, P) % Опитування мережі
Y =
0.8500 1.3114 2.6958 -1.1803
» Y= sim(net,P);
» plot(P,T,P,Y,'о'); % Графічна ілюстрація роботи мережі
Результати та помилка апроксимації лінійної НМ зображені на рис. 6.12, 6.13 відповідно.
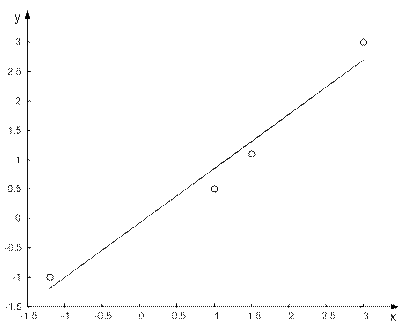
Рисунок 6.12 - Результат апроксимації за допомогою лінійної НМ
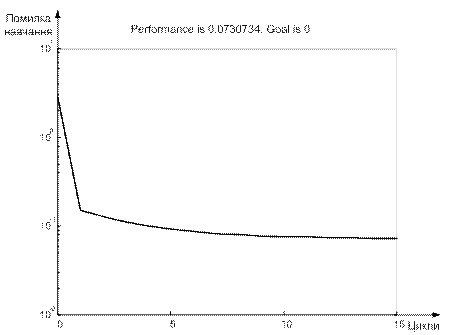
Рисунок 6.13 - Зміна похибки лінійної НМ у процесі навчання
Дата добавления: 2015-10-13; просмотров: 1565;
