Функції пакета Neural Networks Toolbox

Математичний пакет Neural Networks Toolbox (нейронні мережі) може бути використаний для розв’язання безлічі різноманітних завдань, таких як обробка сигналів, нелінійне керування, апроксимація, фінансове моделювання й т.ін. Для кожного типу архітектури й навчального алгоритму штучної НМ є функції ініціалізації, навчання, адаптації, створення, моделювання та ін.

До складу пакета Neural Networks входить більш ніж 150 різноманітних функ­цій, які утворюють своєрідну макромову програмування й дозволяють користувачеві створювати, навчати і використовувати різні НМ. За допомогою команди

»help nnet

можна отримати перелік функцій, що входять до даного пакета.

Для отримання довідки про будь-яку з цих функцій використовується команда:

» help ім’я_функції

Функції пакета Neural Networks Toolbox за своїм призначенням поділяються на ряд груп. Розглянемо деякі з них.

Функції активації (передавальні функції):

- hardlim(X)- порогова функція активації з порогом d = 0; повертає матрицю, розмір якої дорівнює розміру матриці X, а елементи мають значення 0 або 1 залежно від знака відповідного елемента X;

Наприклад:

» X = [0.9 -0.6; 0.1 0.4; 0.2 -0.5; 0 0.5];

» hardlim(X)

ans =

- hardlims(X) - знакова (сигнатурна) функція активації; діє аналогічно hardlim(X) тільки значення -1 або +1;

- logsig(X) – сигмоїдальна (логістична) функція; повертає матрицю, елементи якої є значеннями логістичної функції від елементів матриці X;

- poslin(X) - повертає матрицю значень напівлінійної функції;

- purelin(X) - повертає матрицю значень лінійної функції активації;

- radbas(X) - повертає матрицю значень радіальної базисної функції;

- satlin(X) - повертає матрицю значень напівлінійної функції з насиченням;

- satlins(X) - повертає матрицю значень лінійної функції з насиченням;

- tansig(X) - повертає матрицю значень сигмоїдальної функції (гіперболічний танґенс);

- tribas(X) - повертає матрицю значень трикутної функції належності.

Функції навчання НМ:

- [net tr] = trainbfg(net,Pd,Tl,Ai,Q,TS,VV,TV) – функція навчання, яка реалізує різновид квазіньютонівського алгоритму зворотного поширення помилки (BFGS), і має наступні арґументи: net - назва НМ, яка проходить навчання; Pd - найменування масиву затриманих входів навчальної вибірки; Tl - масив цільових значень виходів; Ai - матриця початкових умов вихідних затримок; Q - кількість навчальних пар в одному циклі навчання (розмір «пачки»); TS - вектор часових інтервалів; VV - порожній ([]) масив або масив перевірочних даних; TV - порожній ([]) масив або масив тестових даних.

Функція повертає навчену НМ net й набір за­писів tr для кожного циклу навчання (tr.epoch - номер циклу, tr.perf - поточна помилка навчання, tr.vperf - поточна помилка для перевірочної вибірки, tr.tperf - поточна помилка для тестової вибірки).

Процес навчання проходить згідно із значеннями наступних параметрів, де в дужках наведені значення за замовчанням:

- net.trainParam.epochs (100) – задана кількість циклів навчання;

- net.trainParam.show (25) – кількість циклів для показу проміжних результатів;

- net.trainParam.goal (0) – цільова похибка навчання;

- net.trainParam.time ( 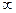) – максимальний час навчання, с;

- net. trainParam.mingrad (10^-6) – цільове значення ґрадієнта;

- net.trainParam.max_fail (5) – максимально припустима кратність
перевищення помилки перевірочної вибірки порівняно з дос­ягнутим мінімальним значенням;

- net.trainParam.searchFcn ('srсhcha') – назва одновимірного­ алгоритму оптимізації, який використовується.

Розглянемо структуру й розміри вищенаведених масивів, які є арґументами функції:

Pd – N0 x Ni x TS – масив комірок, де кожний елемент P{i, j, ts} є матрицею Dij x Q;

Tl – Nl х TS – масив комірок, де кожний елемент P{i, ts} є матрицею Vi x Q;

Ai – Nl х LD – масив комірок, де кожний елемент Ai{i,k}
є матрицею Si x Q,

де Ni=net.numlnputs - кількість входів мережі; Nl = net.numLayers - кількість її шарів; LD=net.numLayerDelays - кількість шарів затримки; Ri=net.inputs{i}.size - розмір i-гo входу; Si=net.layers{i}.size - розмір i-го шару; Vi=net.targets{i}.size - розмір цільового вектора; Dij=Ri*length(net.inputWeights{i,j}.delays) - допоміжна величина).

Для використання функції в НМ, які визначаються користувачем, необхідно:

- установити параметр net.trainFcn = 'trainbfg' (при цьому парамет­ри алгоритму будуть задані за замовчанням);

- установити необхідні значення параметрів (net.trainParam).

Процес навчання зупиняється у випадку виконання будь-якої з наступних умов:

- перевищення заданої кількості циклів навчання (net.trainParam.epochs);

- перевищення заданого часу навчання (net.trainParam.time);

- помилка навчання стала меншою, ніж задана (net.trainParam.goal);

- величина ґрадієнта стала меншою, ніж задана (net.trainParam.mingrad);

- збільшення похибки перевірочної вибірки порівняно з досягнутим мінімальним перевищило задане значення (net.train­.Param.max_fail).

Наприклад:

» Р = [0 1 2 3 4 5]; % Задання вхідного вектора

» Т = [0 0 0 1 1 1]; % Задання цільового вектора

» % Створення й тестування мережі

» net = newff([0 5],[2 1],{'tansig','logsig'},'traincgf');

» a = sim(net,P)

a =

0.0586 0.0772 0.0822 0.0870 0.1326 0.5901

» % Навчання з новими параметрами й повторне тестування

» net.trainParam.searchFcn = 'srchcha';

» net.trainParam.epochs = 50;

» net.trainParam.show = 10;

» net.trainParam.goal = 0.1;

» net = train(net,P,T)

TRAINCGF-srchcha, Epoch 0/50. MSE 0.295008/0.1. Gradient "0.623241/1е-006

TRAINCGF-srchcha. Epoch 1/50, MSE 0.00824365/0.1, Gradient 0.0173555/le-006

TRAINCGF, Performance goal met.

» a = sim(net.P)

a =

0.0706 0.1024 0Л474 0.9009 0.9647 0.9655

У даному прикладі створена багатошарова НМ, яка навчалася з установками за замовчанням, спочатку показала поганий результат відображення навчальної вибірки, але після зміни параметрів і по­вторного навчання мережі результат став більш прийнятним.

- [net tr] = traingd(net,Pd,Tl,Ai,Q,TS,VV) - функція, яка проводить навчання НМ за «класичним» алгоритмом зворотного поширення помилки;

- [net.tr] = trainlm(net,Pd,Tl,Ai,Q,TS,VV) - функція повертає ваги й зсуви НМ, використовуючи алгоритм оптимізації Левенберга-Марквардта;

- [net.tr] = trainoss(net,Pd,Tl,Ai,Q,TS,VV) - функція, яка реалізує різновид алгоритму зворотного поширення помилки з використанням методу січних.

Функції одновимірної оптимізації:

- srchbac – функція реалізує так званий алгоритм перебору
з поверненнями (backtracking);

- srchbre – функція реалізує комбінований метод оптиміза­ції, який поєднує метод золотого перерізу й квадратичну ін­терполяцію;

- srchcha – функція реалізує різновид методу оптимізації
з використанням кубічної інтерполяції;

- srchgol – функція реалізує метод золотого перерізу;

- srchhyb – функція реалізує комбінований метод оптиміза­ції, який поєднує метод дихотомії й кубічну інтерполя­цію.

Функції створення НМ:

- net = newcf(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF) - функція створення каскадної НМ - різновиду багатошарової НМ із зворотним поширенням помилки, яка містить Nl прихованих шарів і має наступні арґументи: PR - R х 2 - матриця мінімальних і максимальних значе­нь R вхідних елементів; Si - розмір i-го прихованого шару, для Nl шарів; TFi - функція активації нейронів i-го шару, за замовчанням 'tansig'; BTF - функція навчання мережі, за замовчанням 'traingd'; BLF - функція настройки ваг й зсувів, за замовчанням 'learngdm'; PF - функція помилки, за замовчанням 'mse';

- net = newff(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF) - функція створення «класичної» багатошарової НМ з навчанням за ме­тодом зворотного поширення помилки;

- net = newfftd(PR,ID,[S1 S2..SNl],{TF1 TF2...TFNl},BTF,BLF,PF) - функція аналогічна newff, але з наявністю затримок за входами (додатковий арґумент ID - вектор вхідних затримок).

- net = newgrnn(P,T,spread) - функція створення узагальнено-реґресійної мережі з арґументами: Р - R х Q - матриця Q вхідних векторів; T - S x Q - матриця Q цільових векторів; spread - відхилення (за замовчанням 1.0);

- net = newlin(PR,S,ID,LR) – функція створення шару лінійних ней­ронів, яка має наступні арґументи: PR - R х 2 - матриця мінімальних і максимальних значе­нь для R вхідних елементів; S - кількість елементів у вихідному векторі; ID - вектор вхідної затримки (за замовчанням [0]); LR - коефіцієнт навчання (за замовчанням 0.01);

- net = newlind(P,T) - функція проектування нового лінійного шару, яка за матрицями вхідних і вихідних векто­рів методом найменших квадратів визначає ваги й зсуви лінійної НМ;

- net = newrbe(P,T,spread) - функція створення мережі з радіальними базисними елементами з нульовою похибкою на навчальній вибірці.

Функції використання НМ:

- [Y,Pf,Af] = sim(net,P,Pi,Ai) - функція, яка моделює роботу НМ з арґументами: net - ім'я мережі; Р - входи мережі; Pi - ма­сив початкових умов вхідних затримок (за замовчанням ну­льові значення); Ai - масив початкових умов затримок шару нейронів (за замовчанням ну­льові значення); повертає значення ви­ходів Y й масиви кінцевих умов затримок.

Арґументи Pi, Ai, Pf, Af використовуються тільки у випадках, коли мережа має затримки за входами або за шарами нейронів.

Структу­ра наведених арґументів наступна:

Р - масив розміром Ni x TS, кожен елемент якого P{i, ts} є матрицею розміром Ri x Q;

Pi - масив розміром Ni x ID, кожен елемент якого Pi{i, k} (i-й вхід у момент ts=k-ID) є матрицею розміром Ri x Q (за замовчанням нульовою);

Ai - масив розміром N1 х LD, кожен елемент якого Ai{i, k} (вихід i-го шару в момент ts=k-LD) є матрицею розміром Si х Q (за замовчанням нульовою);

Y - масив розміром No x TS, кожен елемент якого Y{i, ts} є матрицею розміром Ui x Q;

Pf - масив розміром Ni x ID, кожен елемент якого Pf{i, k} (i-й вхід в момент ts=TS+k- ID) є матрицею розміром Ri х Q;

Af - масив розміром Nl х LD, кожен елемент якого Af{i, k} (вихід i-го шару в момент ts=TS+k-LD) є матрицею розміром Si х Q;

Ni = net.numInputs -кількість входів мережі;

Nl = net.numLayers - кількість її шарів;

No = net.numOutputs - кількість виходів мережі;

ID = net.numInputDelays - вхідні затримки;

LD = net.numLayerDelays - затримки шару;

TS - число часових інтервалів;

Q - розмір набору вхідних векторів;

Ri = net.inputs{i}.size - розмір i-го вектора входу;

Si = net.layers{i}.size - розмір i-го шару;

Ui = net.outputs{i}.size - розмір i-го вектора виходу;

- [net,Y,E,Pf,Af] = adapt(net,P,T,Pi,Ai) – функція адаптації НМ, що виконує адаптацію мережі згідно з установками net.adaptFcn й net.adaptParam, де Е - помилки мережі; Т - цільові значення виходів (за замовчанням нульові); інші аргумен­ти такі, як і у команди sim;

- [net tr] = train(net,P,T,Pi,Ai) – функція здійснює навчання НМ згідно з установками net.trainFcn та net.trainParam, де tr - інформація про виконання процесу навчання (кількість циклів і відповідна помилка навчання).