АНАЛИЗ И СИНТЕЗ РЕГУЛЯТОРОВ АСР С ПОМОЩЬЮ ПАКЕТА MatLab

Требование высокой точности регулирования и высокого

быстродействия, которые предъявляются к современным системам управления обуславливают применение замкнутых систем. Только замкнутые системы позволяют осуществить реализацию двух основных принципов:

- регулируемая величина на выходе системы (скорость, угол, момент, температура и т. д.) должна по возможности точней повторять задающий (входной) сигнал;

- регулируемая величина на выходе системы по возможности не должна зависеть от возмущающих воздействий на объект управления. Такими возмущающими воздействиями могут быть напряжение питания, температура, момент нагрузки, временные зависимости параметров и т.д.

Поэтому основным принципом управления для таких систем является принцип обратной связи, позволяющий осуществить контроль качества регулирования по отклонению управляемого параметра от заданного.

Для исследования таких систем целесообразно применять математическое моделирование с помощью специализированных пакетов, что позволяет сократить затраты на создание системы, уменьшить риск создания неудачного проекта.

Рассмотрим возможности пакета MatLab для анализа и синтеза регуляторов АСР на примере электропривода [2].

В электроприводе в основном применяется три структуры построения [10 ]:

- с промежуточным суммирующим элементом;

- с независимым регулированием параметров;

- с подчиненным регулированием.

Из всех перечисленных способов построения преимущественное распространение получили системы с подчиненным регулированием. В них на выход каждого регулятора W_р1(s) - W_рn(s) подается сигнал с предыдущего каскада (рисунок 1), соответствующий задаваемому уровню регулируемой величины, и сигнал с выхода данного каскада, отвечающий фактическому уровню. Важным достоинством данной структуры является возможность простыми средствами осуществить ограничение любой из координат системы. Для этого достаточно ограничить задание данной координаты.

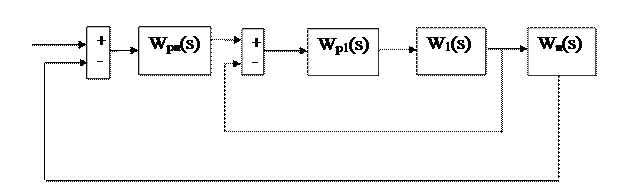
Рисунок 1. Структура схемы подчиненного электропривода

Рассмотрим последовательный синтез регуляторов, начиная с внутреннего контура, который принимаем за первый.

Передаточная функция регулятора подбирается так, чтобы при его включении последовательно с соответствующим звеном системы W₁(s) – W_n(s) была скомпенсирована большая постоянная времени Т и взамен ее действовала меньшая постоянная времени Т₀.

В системах подчиненного регулирования используются регуляторы четырёх типов:

- пропорциональные (П) с передаточной функцией W_p(s)=k_п ;

- интегральные (И) с передаточной функцией W_p(s)= = ;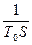

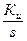- пропорционально интегральные (ПИ) с передаточной функцией W_p(s)=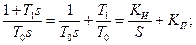
- пропорционально-интегро-дифференциальные (ПИД) с

передаточной функцией

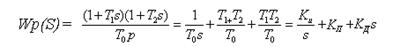
В приведенных выше выражениях:

k_и= - коэффициенты усиления интегрального, пропорционального и дифференциального регуляторов соответственно.

Рассмотрим последовательность синтеза регуляторов в подчиненных системах электропривода.

Для первого контура результирующее эквивалентное звено, состоящее из исходного звена с передаточной функцией W₁(s) и регулятора с передаточной функцией W_p1(s), всегда можно привести к интегрирующему, с передаточной функцией W_РЕЗ.1(s)= 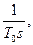то есть регулятор всегда должен быть построен так, чтобы

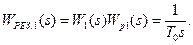(1)

Если в основной цепи имеется интегрирующее звено 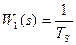, то регулятор должен быть пропорциональным, причем

,

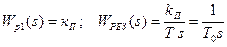где T₀= 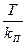; при k_П → 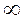постоянная времени Т_о может иметь любое малое значение. После создания замкнутого контура, его передаточная функция будет соответствовать апериодическому звену с малой постоянной времени:

.

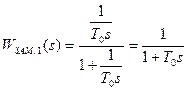На рисунке 2 представлены две модели, в которых система представлена передаточной функцией интегрирующего звена 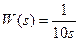. В первой модели регулятором является усилитель с коэффициентом усиления 100, во второй - коэффициент усиления равен 20.

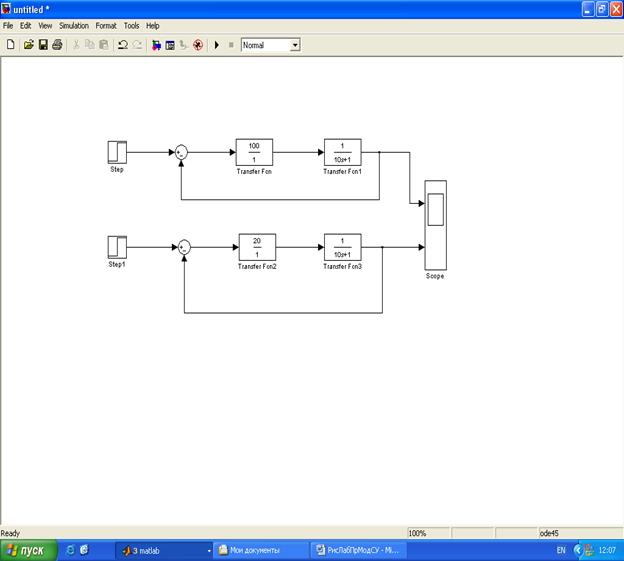
Рисунок 2. Модель интегрирующего звена с регулятором

При создании моделей использованы функциональные блоки из разделов библиотеки:

блок Step из раздела Sources (источники);

блок Sum из раздела Math (математические функции);

блок Transfer Fcn из раздела Continuous (непрерывные );

блок Scope из раздела Sinks (получатели).

Результаты моделирования переходного процесса (рисунок 3) показывают, что вторая модель обладает большей постоянной времени. Это подтверждает вышеприведенные теоретические выводы.

Если исходное звено является апериодическим с передаточной функцией 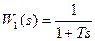, то регулятор должен иметь передаточную функцию, соответствующую ПИ-регулятору,

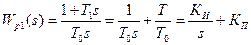
Тогда 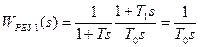, или после охвата обратной связью опять получим .

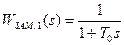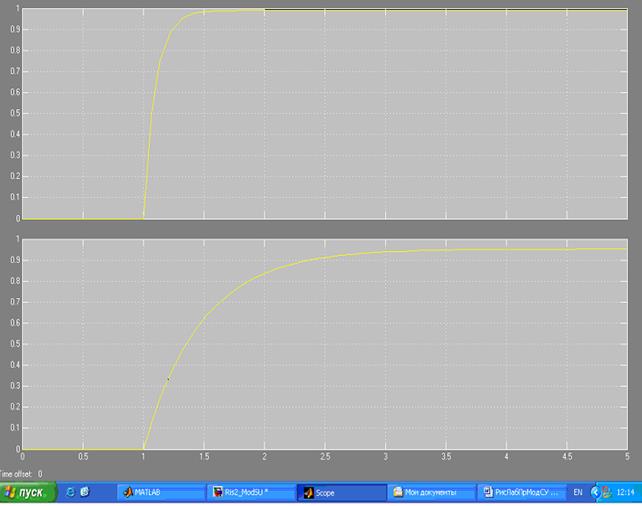
Рисунок 3. Результаты моделирования интегрирующего звена с регулятором

На рисунке 4 представлены две модели. В первой модели реализовано исходное апериодическое звено с передаточной функцией 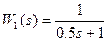. Во второй модели реализован замкнутый контур с ПИ регулятором.

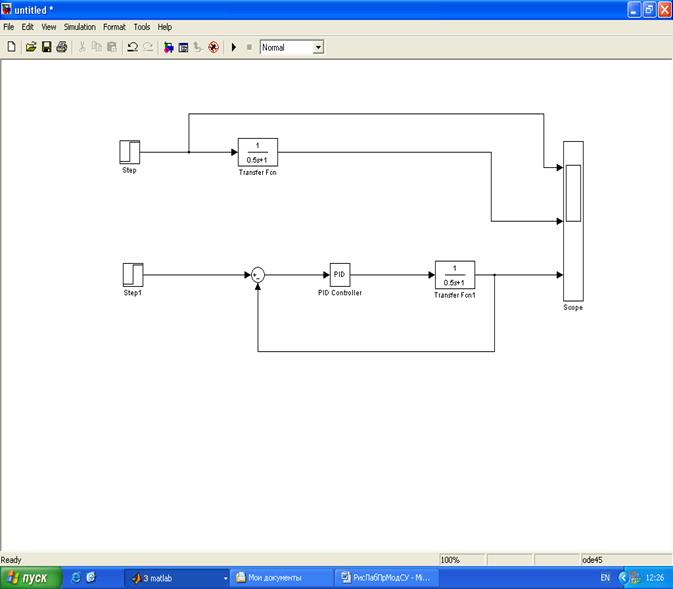
Рисунок 4. Модель апериодического звена с регулятором

При разработке модели АСР (рисунок 4) использован функциональный блок PID (PID - регулятор) который находится в библиотеке SIMULINK в разделе Extras – Additional - Linear Настройка блока PID осуществляется заданием коэффициентов

Результаты моделирования переходного процесса, показанные на рисунке 5, полностью подтверждают теоретические положения, изложенные выше.

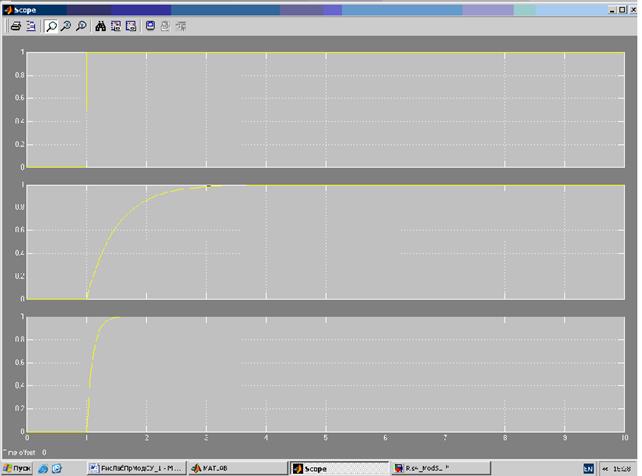
Рисунок 5. Результаты моделирования апериодического звена с регулятором

Если исходная система представляет собой колебательное звено с передаточной функцией 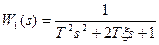, то в соответствии с изложенным подходом регулятор должен быть ПИД – регулятором с передаточной функцией:

.

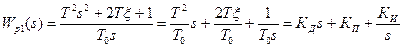В этом случае передаточные функции разомкнутой и замкнутой системы примут вид:

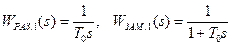
Модель и результаты моделирования для этого случая представлены на рисунках 6 и 7.

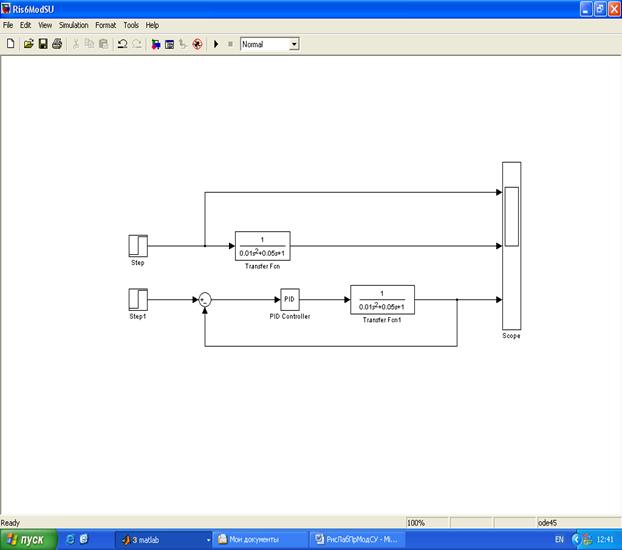
Рисунок 6. Модель колебательного звена с регулятором

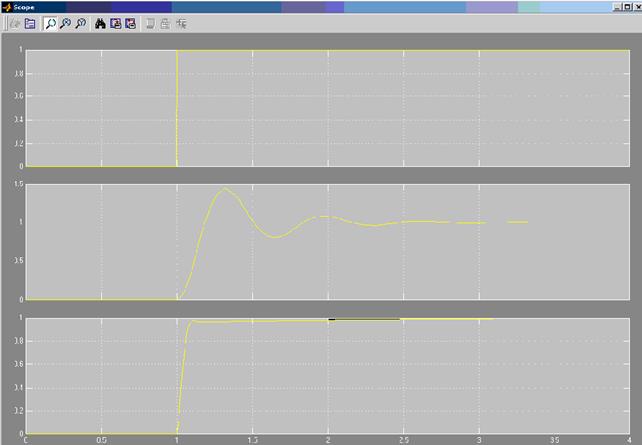
Рисунок 7. Результаты моделирования колебательного звена с регулятором

Таким образом, практически для всех реальных ситуаций первый внутренний контур электропривода с подчиненным управлением можно представить апериодическим звеном с достаточно малой постоянной времени.

Перейдем к рассмотрению второго контура. Если исходное звено второго контура является интегрирующим с передаточной функцией 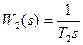, то общая передаточная функция первого и исходного второго звена будет равна:

.

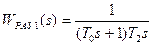Для таких и более сложных систем, о чем будет сказано ниже, регулятор синтезируется таким образом, чтобы в замкнутом контуре получить желаемую передаточную функцию. В качестве желаемых передаточных функций в системах электропривода в основном используются две:

- передаточная функция колебательного звена, настроенного на так называемый технический оптимум (оптимум по модулю, Bietrage-optimum);

- передаточная функция колебательного звена, настроенного на так называемый симметричный оптимум.

В первом случае передаточная функция разомкнутой системы должна иметь вид 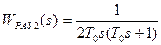, то есть регулятор должен быть пропорциональным с коэффициентом усиления 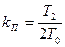. В этом

случае передаточная функция замкнутого контура будет иметь вид:

.

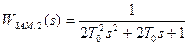Переходная характеристика такого замкнутого звена будет иметь следующие параметры:

- перерегулирование δ = 4,3 %;

- время первого согласования t₁= 4, 71 %;

- время переходного процесса t_р= 8,4 Т_о.

Звено, настроенное на оптимум по модулю, не всегда обеспечивает заданное качество переходного процесса по возмущению. Поэтому внешние контуры в электроприводе (контур скорости или угла) часто настраиваются на симметричный оптимум.

Передаточная функция разомкнутой системы в этом случае должна иметь вид:

,

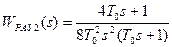то есть в качестве регулятора должна быть использован ПИ-регулятор с передаточной функцией:

.

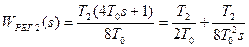Передаточная функция замкнутого контура, настроенного на симметричный оптимум, имеет вид:

,

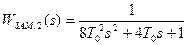Переходная характеристика системы, настроенной на симметричный оптимум, имеет следующие параметры:

- перерегулирование δ = 43 % ;

- время первого согласования t₁ = 3,1 Т_о ;

- время переходного процесса t_p = 16,5 Т_{о .}

Модель рассмотренной системы с П и ПИ регуляторами представлены на рисунке 8. Результаты моделирования переходных процессов в системе при настройке на оптимум по модулю и на симметричный оптимум показаны на рисунке 9.

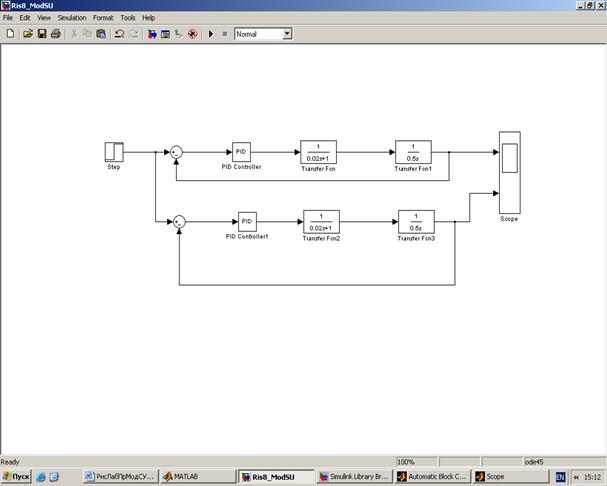
Рисунок 8. Модель АСР, настроенной на оптимум по модулю

и симметричный оптимум

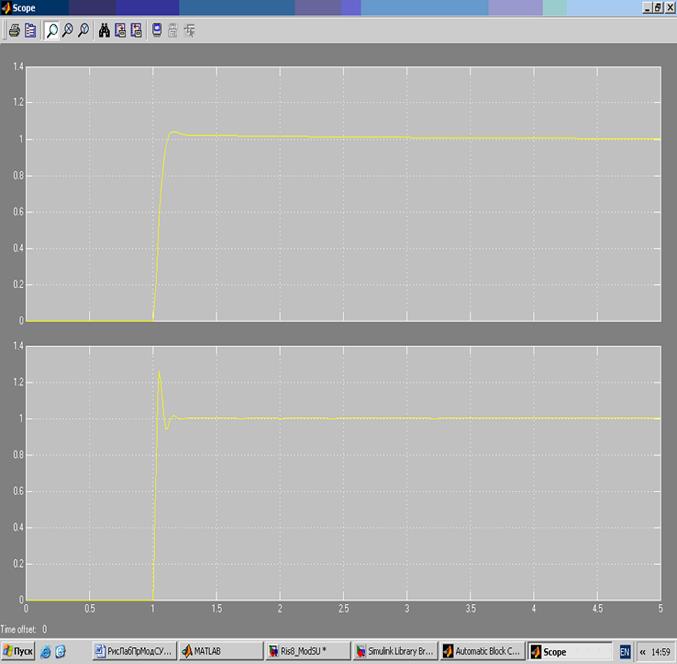
Рисунок 9. Переходные процессы в системе, настроенной на оптимум по модулю и симметричный оптимум

Если исходным звеном второго контура является апериодическое звено с передаточной функцией 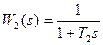, передаточная функция разомкнутого контура с учетом передаточной функции первого контура будет иметь вид:

.

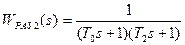В этом случае для реализации в этом контуре оптимума по модулю регулятор должен иметь передаточную функцию следующего вида:

.

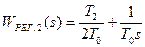Динамические характеристики электропривода могут быть оценены не только параметрами переходного процесса, то есть реакцией системы на скачок входного или возмущающего сигнала, но и рядом других характеристик, из которых наиболее часто используются следующие:

- импульсная характеристика – реакция системы на дельта – функцию. Дельта - функция рассматривается как производная от единичной функции. Изображение по Лапласу дельта - функции равно 1;

- амплитудно-частотная и фазо-частотная характеристики ;

-расположение полюсов и нулей передаточной функции системы.

В версии Matlab 6 приложение Simulink имеет динамическую связь с Control Toolbox - пакетом, позволяющим исследовать вышеперечисленные динамические характеристики электропривода. На эту связь указывает наличие меню Тооls в строке меню модели (рисунок 10).

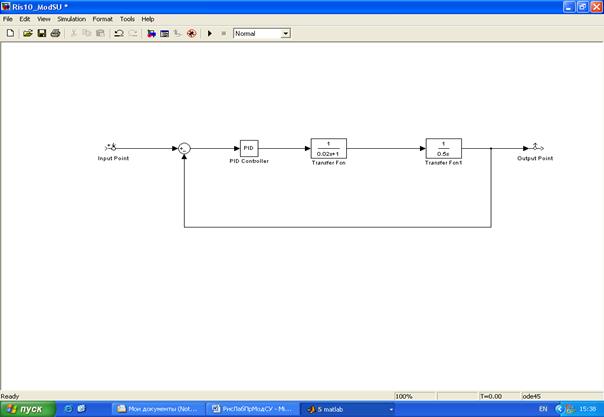
Рисунок 10. Модель, демонстрирующая связь Simulink и

Control Systems Toolbox

Ниже рассматривается динамический анализ системы (рисунок 8), настроенной на симметричный оптимум, с использованием Соntrol System Toolbox. Модель системы показана на рисунке 10. В открывающемся окне меню Тооls выбирается опция Linear Analysis, при этом появляется дополнительная библиотека входных и выходных портов Model Inputs and Outpus (рисунок 11) и пустое окно блока LTI Viewer.

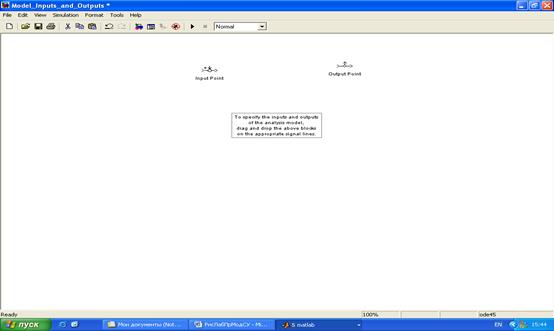
Рисунок 11. Входные и выходные порты модели

Входные и выходные порты, как обычные библиотечные блоки, «перетаскиваются» в окно модели и присоединяются ко входу (входам) и выходу (выходам) исследуемой системы (рисунок 10).

В выпадающем меню окна Edit блока LTI Viewer выбирается опция Plot Configuration, и в открывшемся поле окна настройки задаются методы исследования динамики системы (рисунок 12). В рассматриваемом примере выбраны все перечисленные выше методы.

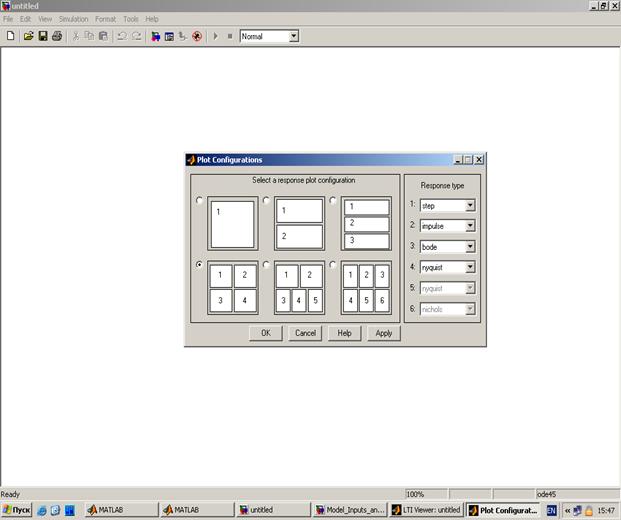
Рисунок 12. Окно настройки представления результатов

моделирования

Последним этапом является проведение моделирования. Для этого в выпадающем меню окна Simulink выбирается опция Get Linearized Model.

Результаты моделирования показаны на рисунке 13.

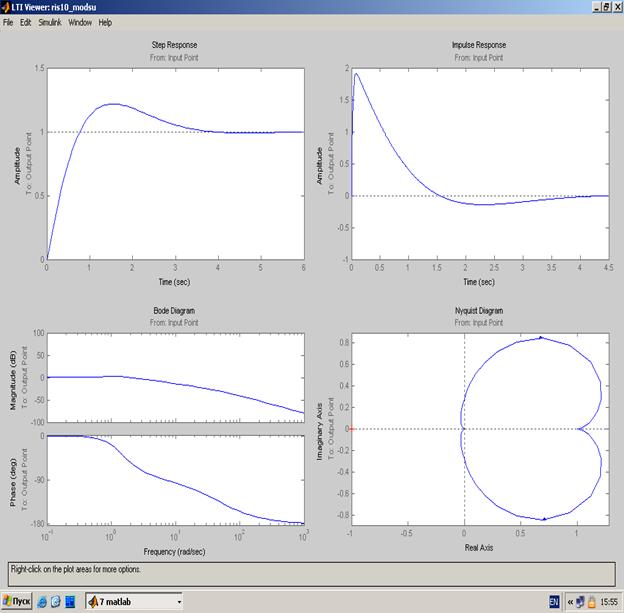
Рисунок 13. Результаты моделирования динамики системы

Все, что сказано до сих пор, касается поведения системы электропривода «в малом», то есть при таких управляющих и возмущающих воздействиях, когда система остается в зоне линейности и ни одна из координат системы не выходит на искусственные или естественные ограничения. На практике системы электропривода в переходных режимах часто работают в режиме ограничения, а в технических заданиях часто оговариваются характеристики именно в этих режимах. Поэтому в дальнейшем таким режимам будет уделено первостепенное внимание. В режимах насыщения аналитические методы исследования системы регулирования встречают различные трудности. Поэтому практически вся теория электропривода посвящена исследованию его работы в линейной зоне. Компъютерное моделирование в этом смысле не имеет ограничений и дает возможности исследования системы в областях ограничения координат, то есть в нелинейной области. Эта особенность компъютерного моделирования широко использована и далее. Исследование системы «в большом» позволяет решать еще одну очень важную задачу - задачу правильного выбора исполнительного двигателя по методу эквивалентных потерь.