УПРАВЛЕНИЯ УГЛОМ ТАНГАЖА ЛА
Угол 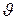 , образуемый продольной осью ЛА с горизонтальной плоскостью, называется углом тангажа. Изменение угла тангажа определяет продольное движение самолета. Система управления углом тангажа самолета служит для обеспечения выдерживания нужной траектории движения в вертикальной плоскости. При этом предусматривается возможность изменения заданного угла тангажа вручную с места пилота или автоматически по сигналам, вырабатываемым системой траекторного управления.
, образуемый продольной осью ЛА с горизонтальной плоскостью, называется углом тангажа. Изменение угла тангажа определяет продольное движение самолета. Система управления углом тангажа самолета служит для обеспечения выдерживания нужной траектории движения в вертикальной плоскости. При этом предусматривается возможность изменения заданного угла тангажа вручную с места пилота или автоматически по сигналам, вырабатываемым системой траекторного управления.
Выходными характеристиками самолета в продольном движении служат углы тангажа 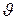 и наклона вектора скорости
и наклона вектора скорости 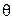 в вертикальной плоскости. Эти углы связаны с углом атаки соотношением
в вертикальной плоскости. Эти углы связаны с углом атаки соотношением 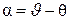 . При управлении углом тангажа происходит два движения: поворот продольной оси самолета вокруг поперечной оси и поворот вектора скорости центра масс в вертикальной плоскости. Поворот самолета вокруг поперечной оси осуществляется под действием продольных моментов, создаваемых рулем высоты, а поворот вектора скорости – под действием нормальных сил. При повороте продольной оси самолета на угол
. При управлении углом тангажа происходит два движения: поворот продольной оси самолета вокруг поперечной оси и поворот вектора скорости центра масс в вертикальной плоскости. Поворот самолета вокруг поперечной оси осуществляется под действием продольных моментов, создаваемых рулем высоты, а поворот вектора скорости – под действием нормальных сил. При повороте продольной оси самолета на угол 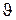 , изменяется угол атаки
, изменяется угол атаки 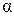 , что приводит к изменению момента статической устойчивости самолета (момент статической устойчивости – часть аэродинамического момента, пропорциональная углу атаки) и к изменению подъемной силы, что является причиной поворота вектора скорости.
, что приводит к изменению момента статической устойчивости самолета (момент статической устойчивости – часть аэродинамического момента, пропорциональная углу атаки) и к изменению подъемной силы, что является причиной поворота вектора скорости.
В случае короткопериодического движения при горизонтальном полете уравнения движения самолета будут иметь вид
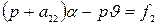 ;
;
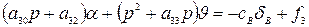 ; (1)
; (1)
где 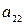 ,
, 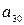 ,
, 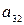 ,
, 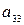 ,
, 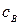 – коэффициенты, зависящие от конструкции самолета,
– коэффициенты, зависящие от конструкции самолета, 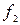 ,
, 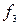 – внешние возмущения,
– внешние возмущения, 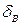 – отклонение руля высоты.
– отклонение руля высоты.
Из уравнений (1) путем преобразования Лапласа при нулевых начальных условиях можно получить передаточные функции самолета по углам тангажа:
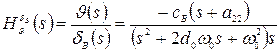 , (2)
, (2)
где 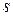 – комплексная переменная преобразования Лапласа,
– комплексная переменная преобразования Лапласа, 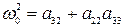 ,
, 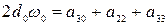 .
.
2.1 Статическая система управления углом тангажа
Рассмотрим статическую систему автоматического управления углом тангажа (рисунок 1), включающую контур управления угловой скоростью и контур управления углом тангажа.

Рисунок 1. Структурная схема статической системы управления углом тангажа
На структурной схеме не показаны внешние возмущения 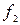 и
и 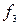 , действующие на ЛА. Закон управления системы берем в виде
, действующие на ЛА. Закон управления системы берем в виде

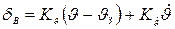 , (3)
, (3)
где 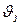 – заданное значение угла тангажа,
– заданное значение угла тангажа, 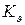 ,
, 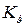 – передаточные числа.
– передаточные числа.
Решая уравнение (1.3) совместно с уравнениями (1.1), получим
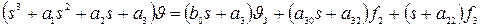 , (4)
, (4)
где 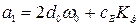 ,
, 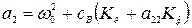 ,
, 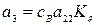 ,
, 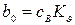 .
.
Рассматриваемая система обладает статической ошибкой. Чтобы определить эту ошибку в уравнении (1.4) примем 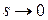 . Тогда при условии
. Тогда при условии 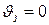 найдем
найдем
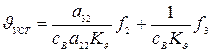 . (5)
. (5)
Отсюда следует, что чем больше передаточное число 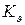 , тем меньше статическая ошибка. Однако при значительном
, тем меньше статическая ошибка. Однако при значительном 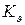 система может стать неустойчивой вследствие динамических погрешностей в элементах автопилота.
система может стать неустойчивой вследствие динамических погрешностей в элементах автопилота.
Выбор параметров системы управления следует производить из условий неискаженного воспроизведения заданного угла тангажа 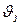 при слабом реагировании на возмущения
при слабом реагировании на возмущения 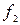 и
и 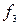 .
.
Будем осуществлять выбор передаточных чисел 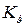 и
и 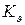 в два этапа. Сначала выберем значение
в два этапа. Сначала выберем значение 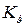 из условия заданного переходного процесса по угловой скорости тангажа во внутреннем контуре САУ. Для выбора передаточного числа
из условия заданного переходного процесса по угловой скорости тангажа во внутреннем контуре САУ. Для выбора передаточного числа 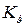 заметим, что наилучшее качество процесса в колебательном звене получается при
заметим, что наилучшее качество процесса в колебательном звене получается при 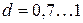 .
.
Передаточная функция для замкнутого внутреннего контура имеет вид
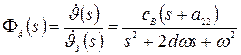 , (6)
, (6)
где 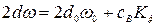 ,
, 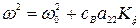 . (7)
. (7)
Исключая из уравнений (1.7) частоту 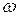 , получим выражение для
, получим выражение для 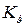
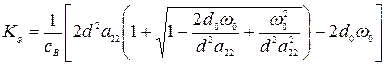 (8)
(8)
Для внешнего замкнутого контура САУ можно написать передаточную функцию
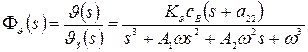 , (9)
, (9)
где 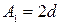 ,
, 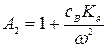 ,
, 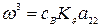 .
.
Известно, что параметры Вышнеградского 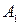 и
и 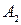 соответствуют оптимальному переходному процессу, если они меняются в пределах от 2 до 3. Поскольку
соответствуют оптимальному переходному процессу, если они меняются в пределах от 2 до 3. Поскольку 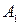 определяется коэффициентом затухания
определяется коэффициентом затухания 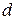 , то следует задать
, то следует задать 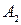 .
.
Из (9) получаем формулу для вычисления 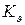 :
:
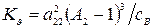 ,
, 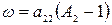 . (10)
. (10)
Полученные выражения определяют безразмерные значения величин. Для получения размерных величин необходимо воспользоваться зависимостями
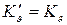 ,
, 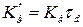 ,
, 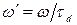 , (11)
, (11)
где 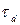 – аэродинамическая постоянная времени ЛА.
– аэродинамическая постоянная времени ЛА.
Размерные передаточные числа 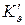 и
и 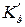 показывают, на какой угол в градусах необходимо отклонить руль высоты при отклонении самолета по углу тангажа на 1° или угловой скорости тангажа 1 град/с.
показывают, на какой угол в градусах необходимо отклонить руль высоты при отклонении самолета по углу тангажа на 1° или угловой скорости тангажа 1 град/с.
2.2 Астатическая система управления углом тангажа
Рассмотрим некоторые вопросы динамики автоматического управления углом тангажа посредством астатического автопилота со скоростной обратной связью (рис. 1.2). Закон управления примем в виде
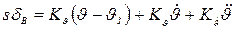 , (12)
, (12)
где 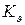 ,
, 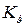 ,
, 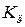 – передаточные числа.
– передаточные числа.

Рисунок 2. Структурная схема продольного канала астатического автопилота со скоростной обратной связью
Для исследования переходных процессов решим уравнение (12) совместно с уравнениями (1):
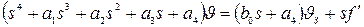 , (14)
, (14)
где 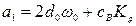 ,
, 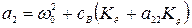 ,
, 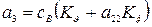 ,
, 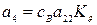 ,
, 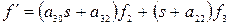 ,
, 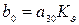 .
.
Поскольку возмущение 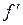 входит под знак оператора дифференцирования, то система не имеет статических погрешностей по отношению к углу тангажа.
входит под знак оператора дифференцирования, то система не имеет статических погрешностей по отношению к углу тангажа.
Рассмотрим передаточную функцию САУ по управляющему сигналу
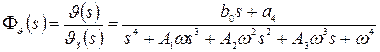 , (15)
, (15)
где 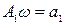 ,
, 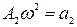 ,
, 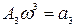 ,
, 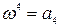 .
.
Выберем параметры систем из условия кратности корней 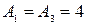 и
и 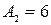 . Передаточные числа при этих условиях будут:
. Передаточные числа при этих условиях будут:
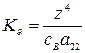 ,
, 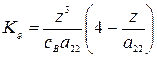 ,
, 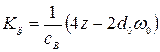 ,
,
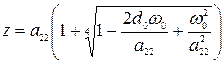 . (16)
. (16)
Размерные передаточные числа:
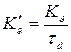 ,
, 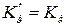 ,
, 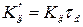 . (17)
. (17)
Для изучения динамических характеристик систем автоматического управления углом тангажа в работе используются две модели, созданные в пакете Simulink системы MATLAB: Lab1_1.mdl – модель статической САУ углом тангажа (рисунок.3) Lab1_2.mdl – модель астатической САУ углом тангажа (рисунок .4).
Числовые значения коэффициентов рассчитаны при следующих входных данных: 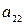 = 2,4;
= 2,4; 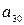 = 0,4;
= 0,4; 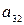 = 38;
= 38; 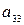 = 4,45;
= 4,45; 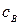 = 49;
= 49; 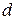 = 1;
= 1; 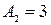 (для статической системы).
(для статической системы).
На схеме приняты следующие обозначения: 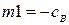 ,
, 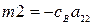 – коэффициенты числителя передаточной функции объекта управления;
– коэффициенты числителя передаточной функции объекта управления; 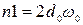 ,
, 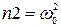 – коэффициенты знаменателя передаточной функции объекта управления;
– коэффициенты знаменателя передаточной функции объекта управления; 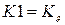 ,
, 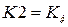 ,
, 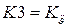 .
.
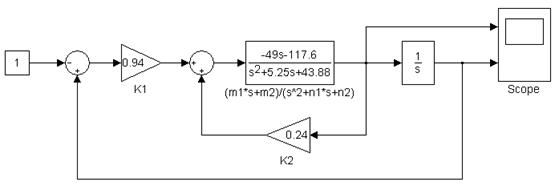
Рисунок .3. Статическая САУ углом тангажа самолета
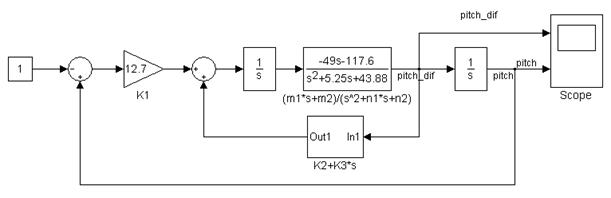
Рисунок 4. Астатическая САУ углом тангажа самолета
Дата добавления: 2015-10-13; просмотров: 7033;
