МОДЕЛИРОВАНИЕ ЦИФРОВЫХ СИСТЕМ УПРАВЛЕНИЯ С ПОМОЩЬЮ ПАКЕТА MatLab
Основным математическим аппаратом теории дискретных систем является z – преобразование. С его помощью решаются задачи анализа устойчивости и качества, а также синтеза систем управления, в состав которых входит цифровой компьютер. Поскольку ввод информации в компьютер осуществляется через определенные интервалы времени, то необходимо разработать специальный метод математического описания и анализа качества цифровых систем управления.
Цифровая система оперирует с данными, получаемыми из непрерывного сигнала путем выборки его значений в равноотстоящие моменты времени. В результате получается временная последовательность данных, называемая дискретным сигналом. Эту последовательность можно преобразовать в область переменной s и, в конечном счете, в область переменной z с помощью соотношения z = esT . Область комплексной переменной z обладает свойствами, очень похожими на свойства области переменной s преобразования Лапласа.
Для анализа устойчивости и качества цифровой системы можно использовать z – преобразование передаточной функции. Таким образом достаточно просто можно определить характеристики замкнутой системы управления, в которой компьютер выполняет функции корректирующего устройства (или регулятора). Для определения положения корней характеристического уравнения также можно использовать метод корневого годографа.
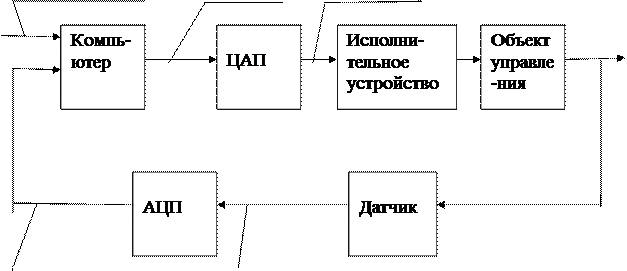
На рисунке 1 приведена функциональная схема одноконтурной цифровой системы управления.
Входной сигнал Выходной сигнал (аналоговый)
(цифровой) Цифровой Аналоговый
Цифровой Аналоговый
Рисунок 1. Функциональная схема цифровой системы управления
Компъютер в этой системе по определенной программе обрабатывает представленную в цифровой форме ошибку и выдает на выходе сигнал также в цифровой форме. Программа может быть написана так, что качество системы в целом будет равно или очень близко к заданному. Многие компъютеры способны принимать и обрабатывать несколько входных сигналов, поэтому цифровые системы управления часто бывают многомерными.
Компъютер получает и обрабатывает сигнал в цифровом (численном) виде, а не в виде непрерывной переменной. В цифровой системе управления обязательно присутствует компъютер, входной и выходной сигнал которого представлены в виде числового кода. Преобразование непрерывного сигнала в цифровую форму осуществляет аналого-цифровой преобразователь (АЦП), как показано на рисунке 1. Выходной сигнал компъютера (цифровой) преобразуется в непрерывную форму с помощью цифроаналогового преобразователя (ЦАП).
Цифровое управление имеет ряд преимуществ, куда относятся: повышенная точность измерений; использование цифровых сигналов (кодов), датчиков и преобразователей и микропроцессоров; меньшая чувствительность к шумам и помехам; возможность легко изменять алгоритм управления в программном обеспечении. Повышенная точность (чувствительность) измерений объясняется тем, что цифровые датчики и устройства работают с маломощными сигналами. Наличие цифровых сигналов дает возможность использовать широкий спектр цифровых устройств и линий коммуникации. Цифровые датчики и преобразователи способны эффективно измерять, передавать сигналы и связывать между собой различные устройства. Кроме того, многие системы объективно являются цифровыми, потому что они работают с импульсными сигналами.
Анализ и синтез дискретных систем управления облегчается при использовании интерактивных компъютерных средств. Многие функции пакета MATLAB, применяемые к непрерывным системам, имеют аналоги, разработанные специально для дискретных систем. Модели объектов в виде дискретных передаточных функций получаются в MATLAB с помощью функции tf. Подобно тому, как это делалось в непрерывных системах. Применение функции tf проиллюстрировано ниже. С помощью функций c2d и d2c можно выполнить преобразование модели системы. Функция c2d преобразует непрерывную систему в дискретную, а функция d2c – наоборот.
Функция tf: sys = tf(num, den, Ts),
где sys - дискретная передаточная функция объекта;
num, den – G( z ) = num/den;
Ts – период квантования.
Функция c2d: [sysd] = c2d(sysc,T, ‘zoh’ ),
где sysd = G(z);
sysc = Gp(s);
T – период квантования;
‘zoh’ – преобразование в дискретную форму с учетом экстраполятора.
Функция d2c: [sysc]= d2c(sysd,T, ‘zoh’ ),
где sysc =Gp(s);
sysd =G(z);
T–период квантования;
‘zoh’ –преобразование в непрерывную форму с учетом экстраполятора.
В качестве примера рассмотрим преобразование объекта управления с передаточной функцией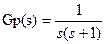 
в дискретную форму с помощью функции c2d. Примем период квантования Т =1 сек.
Использование функции c2d для преобразования G(s) = G (s)G (s) в G(z).
% Этот скрипт преобразует передаточную функцию в
% непрерывной форме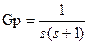 
в дискретную форму при
% периоде квантования Т= 1с.
num=[1]; den= [1 1 0]; sysc=tf(num,den);
T=1;
[sysd]=c2d(sysc,T,’zoh’)
В результате преобразования получим передаточную функцию дискретной системы:
G(z) =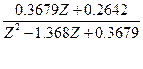 
При моделировании дискретных систем также используются функции step, impulse и lsim. Применение функции step для определения реакции системы у(кТ) на единичный ступенчатый сигнал
[y,T]=step(sys,T)
где у-реакция системы,
Т-вектор времени моделирования, sys =G(z), Т должно быть задано в виде Тi : Тs: Т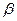 
где Тi - начало моделирования;
Тs - период квантования;
Т 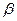- время моделирования.
Пример применения функции step для определения реакции системы у(кТ) на единичный ступенчатый сигнал приведен ниже:
% Этот скрипт вычисляет переходную характеристику у (кТ)
% дискретной системы
%
num=[1]; den=[1 1 0];
sysc=tf(num,den);
sysd=c2d(sysc,1, ‘zoh’);
sys=feedback(sysd,[1]);
T=[0:1:20]; step(sys,T)
Результат вычисления переходной характеристики дискретной системы приведен на рисунке 2.
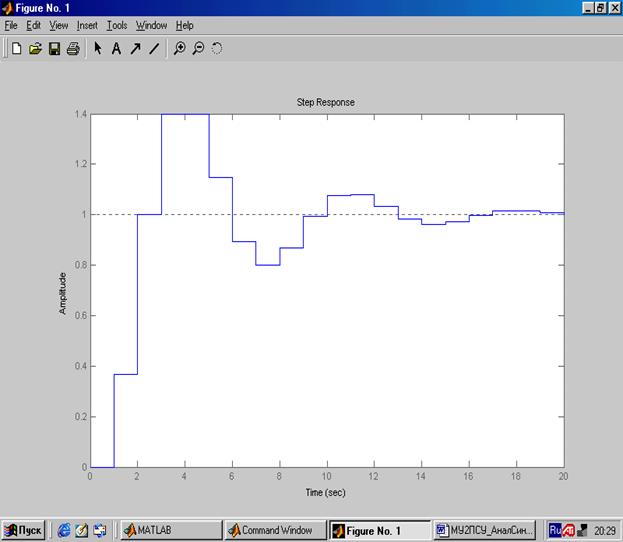
Рисунок 2. Переходная характеристика дискретной системы
% Этот скрипт вычисляет переходную характеристику
% непрерывной системы
%
numg=[1]; deng=[1 1 0]; sysg=tf(numg, deng );
%
[nd,dd]=pade(1,2);
sysp=tf(nd, dd);
sysi=tf([1],[1,0]);
sys1=series(1-sysp,sysi);
%
syso=series(sys1,sysg);sys=feedback(syso,[1]);
t=[0:0.1:20];
step(sys,t)
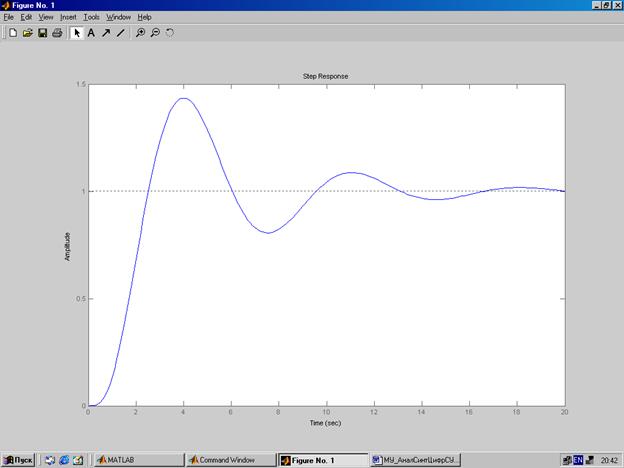
Рисунок 3. Переходная характеристика непрерывной системы
Реакция системы на единичный импульсный сигнал находится с помощью функции impulse, а функция lsim позволяет найти реакцию системы на произвольный входной сигнал. Эти функции применительно к дискретным системам действуют по сути так же, как аналогичные функции для непрерывных систем.
Применение функции impulse для определения реакции системы у(кТ) на единичный импульсный сигнал
[y,T]=impulse(sys,T),
где у-реакция системы,
Т-вектор времени моделирования, sys =G(z), Т должно быть задано в виде 0 : Тs: Т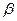 
где Тi - начало моделирования;
Тs - период квантования;
Т 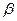- время моделирования.
Применение функции lsim для определения реакции системы у(кТ) на сигнал произвольного вида
[y,T]=lsim(sys,u),
где у-реакция системы,
Т-вектор времени моделирования, sys =G(z),
u- входной сигнал должен квантоваться с тем же периодом, что и при определении sys.
Пример применения функции rlocus к дискретным системам для построения корневого годографа для передаточной функции
G(z0D(z)= k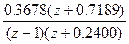 
приведен ниже.
% Этот скрипт строит корневой годограф для
% дискретной системы с передаточной функцией
%
% К(0.3678)(z+0.7189)
%
% (z-1)(z+0.2400)
%
num=[0.3678 0.2644]; den=[1.0000 -0.7600 -0.2400];
sys=tf(num,den);
rlocus(sys); hold on
x=[-1:0.1:1]; y=sqrt(1-x^. 2);
plot(x,y,’---‘,x, y,’---‘)
Дата добавления: 2015-10-13; просмотров: 5745;