УПРАВЛЕНИЯ СКОРОСТЬЮ ПОЛЕТА ЛА

Движение центра масс ЛА должно совершаться по определенной траектории. Выбор траектории полета обусловливается различными факторами, среди которых основными являются безопасность полета, экономичность, тактические соображения и др. При реализации систем управления движением центра масс предусматривают управление высотой полета, боковым отклонением, скоростью полета и числом М.

Скорость самолета в горизонтальном полете определяется из уравнения

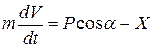. (1)

Сила тяги 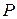и сопротивление 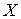зависят от скорости полета. В установившемся режиме полета сила тяги 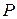равна силе сопротивления 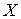, т.е. 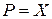. Из этого равенства можно определить величину установившейся скорости полета. В неустановившемся движении величина ускорения 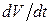и характер её изменения определяются видом функци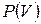и и .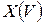

Самолет по отношению к скорости полета может быть устойчивым или неустойчивым в зависимости от взаимного протекания характеристик в точке их пересечения. Полагая, что скорость 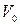соответствует равенству 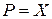и беря линейные члены разложения функци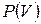й и 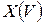в ряды по малым приращениям 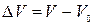, преобразуем уравнение (1) к виду

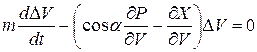. (2)

Если положить приближенно 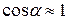, то условие устойчивости самолета по отношению к скорости полета примет вид

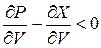. (3)

При нарушении этого неравенства самолет становится неустойчивым по отношению к скорости полета. Для самолетов с поршневым двигателем и дозвуковых самолетов с турбореактивными двигателями условие (3) выполняется. Однако для сверхзвуковых самолетов, особенно на предельной высоте, может быть несколько точек пересечения 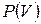и 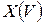, среди которых есть и неустойчивые. Из изложенного следует, что в целях облегчения пилотирования сверхзвуковых самолетов целесообразно применять автоматические системы управления скоростью полета. Необходимость управления скоростью полета возникает также при режимах захода на посадку, при наведении самолета на цели, при полете в строю и др.

Для управления скоростью полета можно воздействовать на тягу двигателя и на руль высоты. Изменение тяги двигателя достигается перемещением ручки управления. При воздействии на руль высоты меняется угол атаки, что ведет к изменению силы сопротивления.

Так как авиационный двигатель, используемый в качестве регулирующего фактора при управлении скоростью полета, формирует требуемую тягу с запаздыванием по отношению к перемещению ручки управления, то его динамические характеристики будут влиять на динамику контура управления скоростью полета. Поэтому при исследовании процессов в контуре управления скоростью полета следует учитывать запаздывание в передаче сигналов через двигатель.

Для автоматического регулирования скорости полета могут быть применены статический и астатический регуляторы (рисунок.1 и 2). В качестве чувствительных элементов в этих регуляторах обычно применяются аэрометрические измерители скорости полета, а сигналы ускорений могут быть получены с помощью акселерометров или дифференцирующих устройств. На этих схемах передаточная функция самолета по скорости полета отображена инерционным звеном, а передаточная функция авиадвигателя – звеном 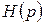, которое в дальнейшем тоже будем считать инерционным, т.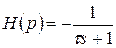е. , где 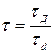, 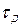– постоянная времени авиадвигателя.

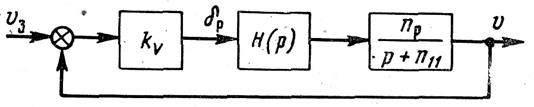
Рисунок 1. Структурная схема статического регулирования скорости полета

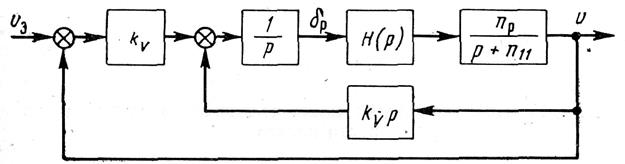
Рисунок 2. Структурная схема астатического регулирования скорости полета

При рассмотрении динамики процессов управления скоростью полета будем полагать, что угловые движения самолета стабилизируются быстродействующим автопилотом. В таком случае математическая модель самолета как объекта управления по скорости полета может быть представлена уравнением

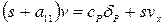, (4)

где 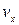– продольные порывы ветра.

Уравнения движения автоматов скорости с учетом передаточной функции авиадвигателя можно представить:

– для статической

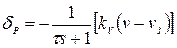; (5)

– для астатической системы

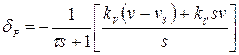, (6)

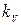где и 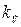– передаточные числа и 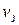– сигнал заданной скорости полета.

Рассмотрим переходные процессы в статическом автомате скорости полета, для чего решим совместно уравнения (4) и (5). Найдем уравнение замкнутой системы

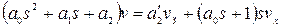, (7)

где ; ; ; .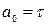

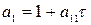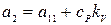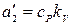Поскольку для неустойчивых по скорости полета самолетов 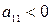, то условиями устойчивости системы будут

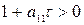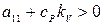; . (8)

Первое условие всегда выполняется, поскольку 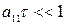. Для выполнения второго условия передаточное число 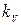должно удовлетворять условию

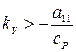. (9)

Поскольку в коэффициенты 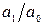и 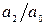уравнения (7) входит только одно передаточное число 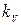, то отсутствует неопределенность в его выборе. Поэтому следует взять достаточно большое значение числа 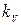, при котором обеспечивается устойчивость системы, но при этом тяга двигателя при работе регулятора меняется в приемлемых пределах. Большое значение передаточного

числа выбирать не следует, так как при глубоком изменении тяги двигателя может произойти срыв пламени в двигателе и его выключение.

В случае астатического автомата скорости полета, решая совместно уравнения (4) и (6), получаем

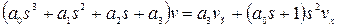, (10)

где ; ; ; .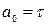

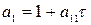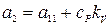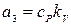Для устойчивости системы необходимо удовлетворить условиям:

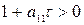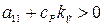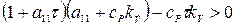; ; . (11)

Отсюда следует, что если 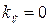, то система структурно неустойчива. Можно выбрать такие передаточные числа 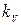и 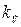, при которых переходные процессы будут удовлетворительны.

Для выбора передаточных чисел астатического автопилота запишем передаточную функцию замкнутой системы при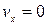

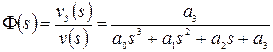. (12)

Поделим числитель и знаменатель функции 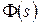на 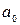и приблизим полученную функцию к стандартной

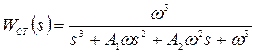. (13)

Условия совпадения данных передаточных функций сводятся к равенствам

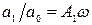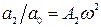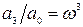, , (14)

или с учетом выражений (2.10)

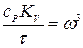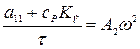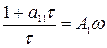; ; , (15)

где 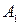и 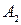– параметры Вышнеградского, 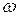– собственная частота системы.

Из уравнений (15) находим:

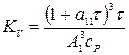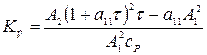; . (16)

Системы автоматического управления скоростью полета изучались с помощью следующих моделей: Lab2_1.mdl – модель статической САУ скоростью полета (рисунок .3) Lab2_2.mdl – модель астатической САУ скоростью полета (рисунок 4).

Числовые значения коэффициентов рассчитаны при следующих входных данных: 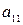= -0,01; 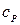= 0,02; 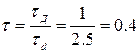; 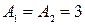(для астатической системы).

На схеме приняты следующие обозначения: , .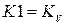

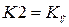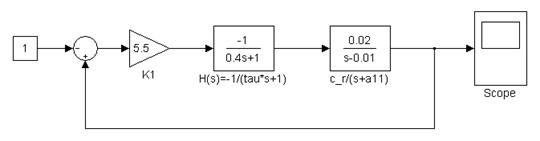
Рисунок.3. Статическая САУ скоростью полета самолета

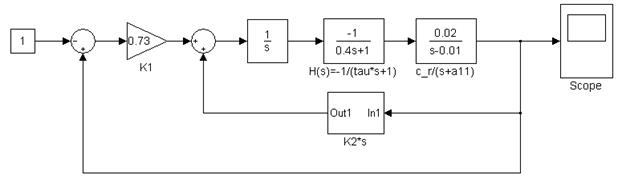
Рисунок 4. Астатическая САУ скоростью полета самолета