Персептрони. Прагнучи відтворити функції людського мозку, дослідники створили прості апаратні (а пізніше програмні) моделі біологічного нейрона й системи його з'єднань

Прагнучи відтворити функції людського мозку, дослідники створили прості апаратні (а пізніше програмні) моделі біологічного нейрона й системи його з'єднань. Перше систематичне вивчення штучних НМ було започатковане Макалохом і Пітсом 1943 р. Пізніше вони досліджували мережні парадигми для розпізнавання зображень, що піддають зрушенням і поворотам, використовуючи при цьому просту нейронну модель, показану на рис. 6.6. Елемент S множить кожний вхід х_i на вагу w_i і підсумовує зважені входи. Якщо ця сума більша за задане граничне значення, вихід дорівнює одиниці, у протилежному випадку - нулю. Ці системи (і безліч подібних до них) одержали назву персептронів. Вони складаються з одного шару штучних нейронів, з'єднаних за допомогою вагових коефіцієнтів з безліччю входів.

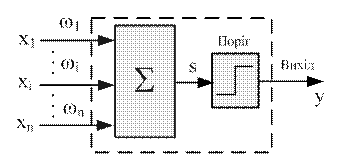
Рисунок 6.6 - Персептронний нейрон

Розглянемо як приклад тринейронний персептрон (рис. 6.7), нейрони якого мають активаційну функцію у вигляді одиничного стрибка.

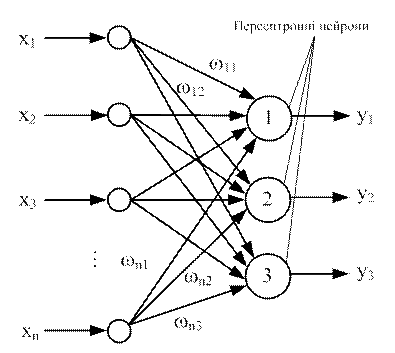
Рисунок 6.7 - Персептрон з багатьма виходами

На n входів надходять вхідні сигнали, що проходять по синапсам на три нейрони, які утворюють єдиний шар цієї мережі й видають три вихідні сигнали:

.

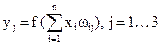Усі вагові коефіцієнти синапсів одного шару нейронів можна звести в матрицю W, у якій кожний елемент 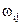задає величину i-го синаптичного зв'язку j-гo нейрона. Таким чином, процес, що відбувається в НМ, може бути записаний у матричній формі:

Y=f(XW),

де X і Y - відповідно вхідний й вихідний сигнальні вектори-рядки; f(S) - активаційна функція, що застосовується для кожного елемента вектора S.

На рис. 6.8 зображений двошаровий персептрон, отриманий з персептрона, зображеного на рис. 6.7, шляхом додавання другого шару, що складається з двох нейронів.

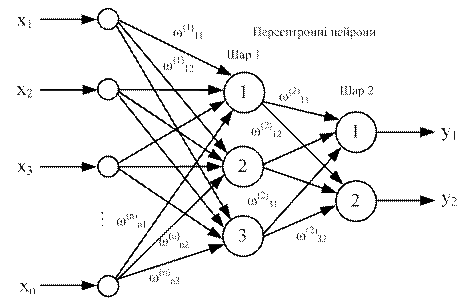
Рисунок 6.8 - Двошаровий персептрон

Фактично така Q-шарова НМ еквівалентна мережі з одним прихованим шаром з ваговою матрицею єдиного шару :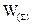

.

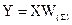Робота персептрона зводиться до класифікації (узагальнення) вхідних сигналів, що належать n-вимірному простору за деяким числом класів. З математичної точки зору це відбувається шляхом розбиття простору площинами. Для випадку одношарового персептрона:

.

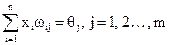Кожна отримана область є областю визначення окремого класу. Число таких класів для персептрона не перевищує 2ⁿ, де n- число його входів. Однак не всі з класів можуть бути виділені даною НМ (проблема виключного «АБО»).

Навчання персептрона зводиться до формування ваг зв'язків між першим й другим шарами відповідно до наступного алгоритму:

- ініціалізація елементів вагової матриці (зазвичай невеликими випадковими значеннями);

- подання на входи одного з вхідних векторів, які мережа повинна навчитися розрізняти й обчислити його вихід;

- якщо вихід правильний, продовжити навчання НМ, інакше – обчислити різницю між ідеальним d і отриманим Y значеннями виходу d=d–Y, модифікувати ваги 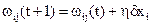, де t, (t+1) - номери поточної й наступної ітерацій відповідно; h - коефіцієнт швидкості навчання (0 <h< 1); i - номер входу; j - номер нейрона в шарі; при d>Y вагові коефіцієнти збільшуються, зменшуючи помилку, у протилежному випадку – зменшуються.

- повернутися до навчання НМ пред'являючи на різних ітераціях по черзі у випадковому порядку всі можливі вхідні вектори, доки мережа не перестане помилятися.