Прогнозування значень процесу
Розглянемо наступні приклади прогнозу за допомогою методу вікон. Нехай є сигнал (функція часу), який описується наступним співвідношенням:
x(t) = sin(4pt),
й підлягає дискретизації з інтервалом 0.025 с.
Побудуємо лінійну НМ, яка дозволяє прогнозувати майбутнє значення подібного сигналу за 5 попередніми. Розв’язок даної задачі наведено нижче.
» t = 0:0.025:5; % Задання діапазону часу від 0 до 5 секунд
» x = sin(4*pi*t); % Передбачуваний сигнал
» Q = length(x); % Кількість значень передбачуваного сигналу
» % Створення вхідних векторів
» Р = zeros(5,Q); % Створення нульової матриці Р розміром 5 x Q (5- кількість попередніх значень)
» % Елементам i-го рядку матриці P, починаючи з i+1-го, присвоюються Q-(i+1) значення масиву x, починаючи з першого значення (P(i,i+1:Q) = x(1,i:(Q-(i+1)))); i=1..5
» P(1,2:Q) = x(1,1:(Q-1));
» P(2,3:Q) = x(1,1:(Q-2));
» P(3,4:Q) = x(1,1:(Q-3));
» P(4,5:Q) = x(1,1:(Q-4));
» P(5,6:Q) = x(1,1:(Q-5));
» s = newlind(P,x); % Створення нової мережі з ім'ям s
» y = sim(s,P); % Розрахунок прогнозованих значень
» % Створення графіків вихідного сигналу й прогнозу
» plot(t,y,t,x, '*');
» xlabel('Час');
» ylabel('Прогноз - Сигнал +');
» title('Вихід мережі й дійсні значення');
» % Розрахунок і створення графіка помилки прогнозу
» е = x - у;
» plot(t,e);
» xlabel('Час');
» уlabel('Помилка');
» title('Сигнал помилки');
У даному випадку мережа створювалась за допомогою функції newlind, для якої не потрібно проводити додаткового навчання.
Виходячи з графіків результатів прогнозування, що наведені на рис. 6.14, 6.15, точність прогнозу з використанням лінійної мережі можна вважати прийнятною.
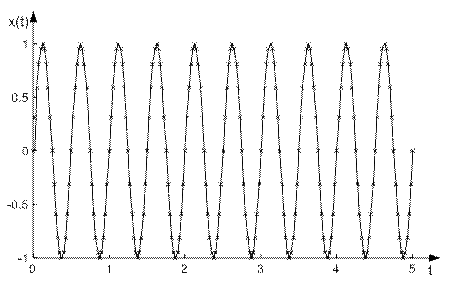
Рисунок 6.14 - Прогнозовані значення
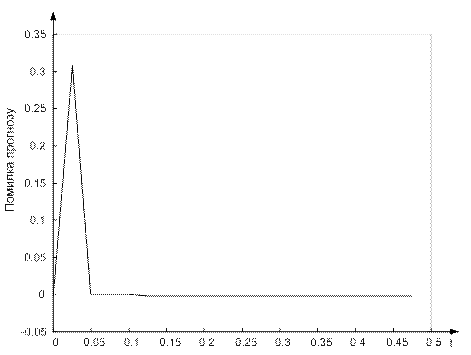
Рисунок 6.15 - Помилка прогнозу
Розглянемо практичну задачу - задачу прогнозування енергоспоживання на 1 день уперед.
Припустимо, є база даних, яка містить значення коефіцієнта енергоспоживання за останні 21 дні (табл. 6.2). Найпростіший варіант у даному випадку - спробувати побудувати прогноз завтрашнього енергоспоживання на основі коефіцієнтів енергоспоживання за останні декілька днів. Зрозуміло, що прогнозуюча НМ повинна мати лише один вихід і стільки входів, скільки попередніх значень буде використовуватися для прогнозу - наприклад, 4 останні значення.
Таблиця 6.2 - Значення коефіцієнтів енергоспоживання за 21 день
| День | |||||||||||
| Коефіцієнт | 1.81 | 3.22 | 3.22 | 1.90 | 0.48 | 0.29 | 1.59 | 3.41 | 4.42 | 4.10 | 3.10 |
| День | |||||||||||
| Коефіцієнт | 2.49 | 2.8 | 3.61 | 4.2 | 4.3 | 4.29 | 4.69 | 5.41 | 5.82 | 5.41 | ? |
Складемо навчальний приклад, у якому вхідними значеннями НМ будуть коефіцієнти енергоспоживання за 4 послідовні дні, а бажаним виходом НМ – відомий коефіцієнт на п’ятий день.
Підготовка навчальної вибірки складається з наступних операцій за допомогою методу вікон, де ширина вікна дорівнює 4:
- скопіювати стовпчик даних значень коефіцієнта в 4 сусідніх стовпчика;
- зсунути другий стовпчик на одну комірку вгору, третій стовпчик - на 2 комірки вгору й т.д.
Процес підготовки зображений на рис. 6.16 - тепер кожен рядок таблиці являє собою навчальний приклад, де перші 4 числа - вхідні значення НМ, а п’яте число - бажане значення виходу мережі. Виняток становлять останні 4 рядки, де даних недостатньо - ці рядки не враховуються під час тренування НМ.
У четвертому знизу рядку задані всі 4 вхідні значення, але невідоме значення виходу мережі. До цього рядка застосуємо навчену НМ й отримаємо прогноз на наступний 22 день.
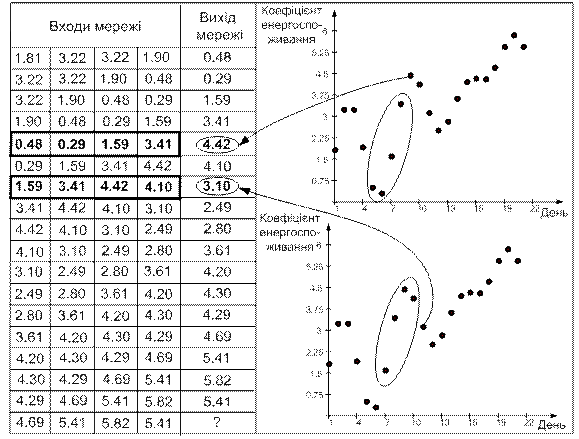
Рисунок 6.16 - Ілюстрація створення навчальної вибірки
Побудуємо лінійну НМ, яка дозволяє прогнозувати майбутнє значення коефіцієнта енергоспоживання за 4 попередніми значеннями. Розв’язок даної задачі в математичному пакеті Мatlab наведено нижче:
» % Створення навчальної вибірки
» n=5:1:21;
» % Задання вхідних векторів
» P = [1.81 3.22 3.22 1.9 0.48 0.29 1.59 3.41 4.42 4.1 3.1 2.49 2.8 3.61 4.2 4.3 4.29;
3.22 3.22 1.9 0.48 0.29 1.59 3.41 4.42 4.1 3.1 2.49 2.8 3.61 4.2 4.3 4.29 4.69;
3.22 1.9 0.48 0.29 1.59 3.41 4.42 4.1 3.1 2.49 2.8 3.61 4.2 4.3 4.29 4.69 5.41;
1.9 0.48 0.29 1.59 3.41 4.42 4.1 3.1 2.49 2.8 3.61 4.2 4.3 4.29 4.69 5.41 5.82];
» % Задання вихідного вектора
» x = [ 0.48 0.29 1.59 3.41 4.42 4.1 3.1 2.49 2.8 3.61 4.2 4.3 4.29 4.69 5.41 5.82 5.41];
» s = newlind(P,x); % Створення нової мережі з ім'ям s
» у = sim(s,P); % Розрахунок прогнозованих значень
» % Створення графіків вихідного сигналу й прогнозу
» z = sim(s,[4.69; 5.41; 5.82; 5.41;]) % Розрахунок прогнозу на наступний день
z =
4.3422
» plot(n,y,n,x,'x',22,z);
» xlabel('День');
» ylabel('Коефіцієнт енергоспоживання');
» title('Вихід мережі, дійсні значення);
» % Розрахунок і створення графіка помилки прогнозу
» е = у-x;
» plot(n,e);
» xlabel('День');
» уlabel('Помилка');
» title('Сигнал помилки');
Прогноз коефіцієнта енергоспоживання, отриманий за допомогою лінійної НМ, та зміна його помилки наведені на рис. 6.17 і 6.18 відповідно.
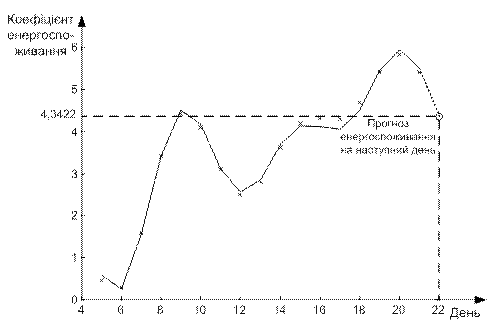
Рисунок 6.17 - Результат прогнозу коефіцієнта енергоспоживання на наступний день за допомогою лінійної НМ
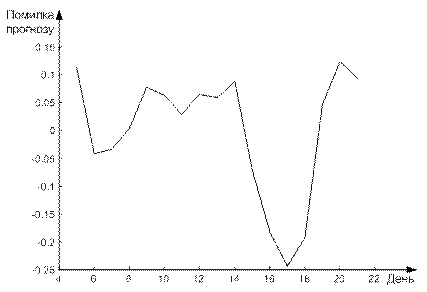
Рисунок 6.18 - Помилка прогнозу коефіцієнта енергоспоживання
З цього прикладу видно, що обсяг навчальної вибірки залежить від вибраної кількості входів мережі. При виборі числа входів НМ слід враховувати це, вибираючи розумний компроміс між глибиною прогнозу (число входів мережі) та якістю навчання (обсяг тренувального набору).
У попередніх прикладах настройка НМ виконувалась адаптивно. Відміна такої настройки від тієї, яка виконується, наприклад, за допомогою методу зворотного поширення похибки, полягає в тому, що вектори навчальної вибірки надходять на вхід мережі не всі «одночасно», а послідовно один за одним. При цьому після подання чергового вектора проводиться кориґування вагових коефіцієнтів та зміщень і може бути проведене опитування мережі, потім процес повторюється. Адаптивна настройка особливо зручна під час роботи мережі в «реальному» масштабі часу.
Розглянемо приклад задачі прогнозування значень сигналу за 5 попередніми значеннями з використанням такої адаптивної настройки для лінійної НМ.
Нехай вихідний сигнал визначений на інтервалі часу від 0 до 6 с, при цьому при 0 < t < 4 від описується співвідношенням x(t) = sin(4t), а при 4 < t < 6 – співвідношенням x(t) = sin(8t). Графік такого сигналу наведений на рис 6.19.

Рисунок 6.19 - Вихідний сигнал
Описаний вище вихідний сигнал у математичному пакеті Matlab створюється за допомогою наступної системи команд:
» time1 = 0:0.05:4;
» time2 = 4.05:0.024:6:
» time = [time1 time2];
» % T визначає вихідний сигнал
» T = con2seq([sin(timel*4*pi) sin(time2*8*pi)]); % Об’єднання в один масив значень вихідного сигналу для інтервалів часу time1 , time2
» % Графік вихідного сигналу:
» plot(time,cat(2,T{:}));
» xlabel('Час');
» ylabel(‘Вихідний сигнал');
» title('Прогнозований сигнал');
Для прогнозу значень сигналу створимо лінійну НМ та виконаємо її адаптивне настроювання за допомогою наступної послідовності команд:
» % Вхідний і цільовий сигнал, який прогнозується, однакові:
» Р = Т;
» % Задання коефіцієнта навчання
» 1r = 0.1;
» % Для прогнозу використовують 5 попередніх значень
» delays = [1 2 3 4 5];
» net = newlin(minmax(cat(2,P{:})),1,delays,lr); % Створення лінійної НМ
» [net,y,e] = adapt(net,P,T); % Адаптивна настройка мережі
» % Графіки вихідного сигналу та прогнозу
» plot(time,cat(2,y{:}),time,cat(2,T{:}),'--')
» xlabel('Час');
» ylabel('Прогнозований сигнал');
» title('Вихідний сигнал і прогноз');
Розглянемо нижченаведений процес створення й цикл адаптивної настройки багатошарової мережі для прогнозу значень сигналу:
» % Створення багатошарової мережі
» ne = newfftd(minmax(cat(2,P{:})),delays,[5 1], {'tansig' 'purelin'},'trainbr');
» k=5; % Кількість циклів навчання
» % Цикл адаптивної настройки багатошарової мережі
» while (k>=1)
[net,y,e] = adapt(net,P,T);
k=k-1;
end;
Графіки вхідного сигналу й прогнозу для вищерозглянутого прикладу, які отримані за допомогою адаптивної настройки лінійної та класичної багатошарової НМ, наведені на рис. 6.20.
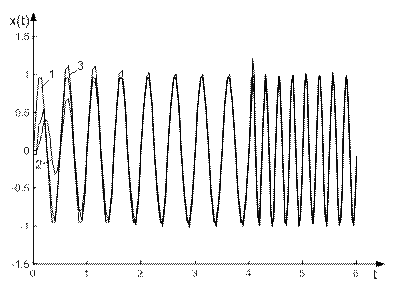
Рисунок 6.20 - Графіки вихідного сигналу (1) та прогнозу лінійної (2) й багатошарової (3) НМ
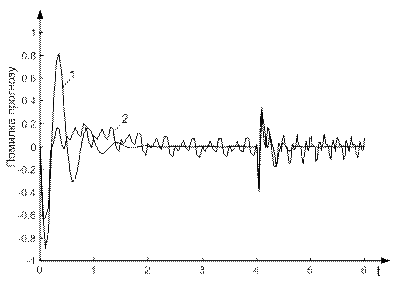
Рисунок 6.21 - Графік помилки прогнозу лінійної (1) й багатошарової (2) НМ
З графіків на рис. 6.20-6.21 видно, що отриманий результат прогнозу можна вважати задовільним.
Дата добавления: 2015-10-13; просмотров: 991;
