Персептрони
Намагаючись відтворити функції людського мозку, дослідники створили прості апаратні (а пізніше програмні) моделі біологічного нейрона і системи його з'єднань. Коли нейрофізіологи досягли більш глибокого розуміння нервової системи людини, ці спроби стали сприйматися як дуже грубі апроксимації. Проте на цьому шляху були досягнуті вражаючі результати, стимулюючі подальші дослідження, що призвели до створення складніших мереж. Перше систематичне вивчення штучних нейронних мереж було зроблено в 1943 р. Пізніше Маккалоx і Піттс досліджували мережні парадигми для розпізнавання зображень, що піддаються зсувам і поворотам, використовуючи при цьому просту нейронну модель (рис. 7.1.). Елемент  домножує кожний вхід хі на вагу
домножує кожний вхід хі на вагу 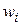 і сумує входи.
і сумує входи.
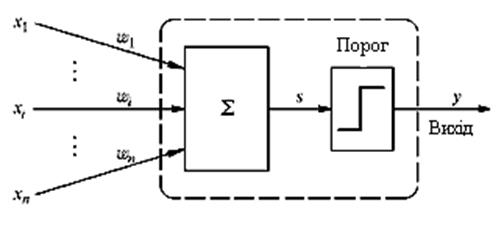 |
Рис. 7.1. Персептроний нейрон
Якщо ця сума більше заданого порогового значення, вихід рівний одиниці, інакше – нулю. Ці системи (і багато їм подібних) одержали назву персептронів.
У 60-ті роки персептрони викликали великий інтерес і оптимізм. Розенблатт довів теореми про навчання персептронів, що приводяться нижче. Уідроу дав ряд переконливих демонстрацій систем персептронного типу, і дослідники у всьому світі прагнули вивчити можливості цих систем. Початкова ейфорія змінилася розчаруванням, коли виявилося що персептрони не здатні навчитися рішенню ряду простих задач. Мінський строго проаналізував цю проблему і показав, що є жорсткі обмеження на те, що можуть виконувати одношарові персептрони, і відповідно чому вони можуть навчатися. Оскільки у той час методи навчання багатошарових мереж не були відомі, дослідники перейшли в більш багатообіцяючі області, і дослідження в області нейронних мереж занепали. Відкриття методів навчання багатошарових мереж більшою мірою, ніж який-небудь інший чинник, вплинуло на відродження інтересу.
Розглянемо як приклад трьохнейронний персептрон (рис. 7.2), нейрони якого мають активаційну функцію у вигляді одиничного стрибка.
На 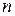 входів поступають вхідні сигнали, що проходять по синапсах, на три нейрони, створюючі єдиний шар цієї мережі і видаючи три вихідні сигнали:
входів поступають вхідні сигнали, що проходять по синапсах, на три нейрони, створюючі єдиний шар цієї мережі і видаючи три вихідні сигнали:
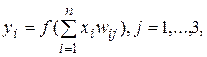 (7.1)
(7.1)
Очевидно, що всі вагові коефіцієнти синапсів одного шару нейронів можна звести в матрицю W, в якій кожний елемент Wij задає величину і-ому синаптичному зв'язку j-гo нейрона.
Таким чином, процес, що відбувається в нейронній мережі, може бути записаний в матричній формі:
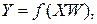 (7.2)
(7.2)
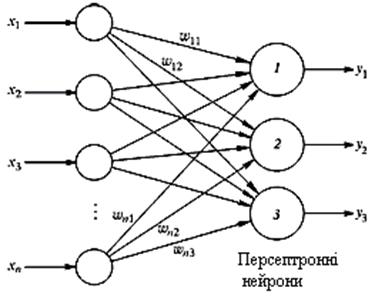 |
Рис. 7.2. Персептрон з багатьма виходами
де: X і Y – відповідно вхідній і вихідний сигнальні вектори (тут і далі під вектором розуміється вектор-рядок),
f(S) – активаційна функція, вживана до компонентів вектора S.
На рисунку 7.3 представлений двошаровий персептрон, отриманий з персептрона з рисунку 7.2 шляхом додавання другого шару, що складається з двох нейронів.
Доречно відзначити важливу роль нелінійності активаційоної функції, оскільки, якби вона не володіла даними якостями або не входила в алгоритм роботи кожного нейрона, результат функціонування будь-якої Q-шарової нейронної мережі з ваговими матрицями W(q) для кожного шару q=1,...,Q зводився б до перемножування вхідного вектора сигналів X на матрицю:
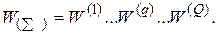 (7.3)
(7.3)
Фактично така Q-шарова нейронна мережа еквівалентна мережі з одним прихованим шаром і з ваговою матрицею єдиного шару 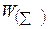 :
:
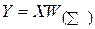 (7.4)
(7.4)
Робота персептрона зводиться до класифікації (узагальнення) вхідних сигналів, що належать 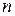 -мірному гіперпростору, за деяким числом класів. З математичної точки зору це відбувається шляхом розбиття гіперпрпростору гіперплощинами.
-мірному гіперпростору, за деяким числом класів. З математичної точки зору це відбувається шляхом розбиття гіперпрпростору гіперплощинами.
Для випадку одношарового персептрона:
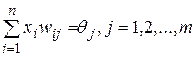 (7.5)
(7.5)
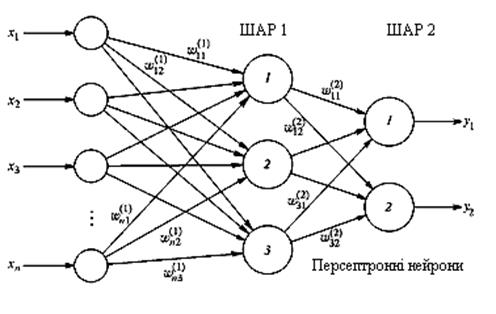 |
Рис. 7.3. Двошаровий персептрон
Кожна одержана область є областю визначення окремого класу. Число таких класів для персептрона не перевищує 2 n, де n – число його входів. Проте не всі класи можуть бути розділені даною нейронною мережею. Наприклад, одношаровий персептрон, що складається з одного нейрона з двома входами, не може реалізувати логічну функцію “ВИКЛЮЧНЕ АБО”, тобто не здатний розділити площину (двовимірне гіперпростір) на дві напівплощини так, щоб здійснити класифікацію вхідних сигналів по класах А і B (табл. 7.1).
Рівняння мережі для цього випадку:
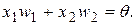 (7.6)
(7.6)
Це – рівняння прямої (одновимірної гіперплощини), котра ні за яких умов не може розділити площину так, щоб точки з нескінченності вхідних сигналів, що належать різним класам, виявилися по різні сторони від прямої (рис. 7.4). Неможливість реалізації одношаровим персептроном цієї функції одержала назву “проблеми ВИКЛЮЧНОГО АБО”.
Відзначимо, що функції, які не реалізуються одношаровим персептроном, називаються лінійно нероздільними.
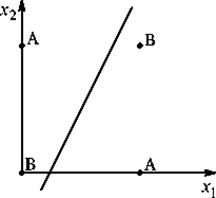
Рис. 7.4. Лінійна нероздільність функції “ВИКЛЮЧНОГО АБО”
Таблиця 7.1. Логічна функція “Виключне АБО”
| х1 \ х2 | ||
| В | А | |
| А | В |
Навчання персептрона зводиться до формування вагів зв'язків між першим і другим (рис. 7.3) шарами відповідно до наступного алгоритму.
Крок 1. Проініціалізувати елементи вагової матриці (звичайно невеликими випадковими значеннями).
Крок 2. Подати на входи один з вхідних векторів, які мережа повинна навчитися розрізняти, і обчислити її вихід.
Крок 3. Якщо вихід правильний, перейти до кроку 4.
Інакше – обчислити різницю між ідеальним d і отриманим Y значеннями виходу:
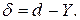 (7.7)
(7.7)
Модифікувати вагу відповідно до формули:
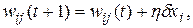 (7.8)
(7.8)
де: 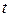 і
і 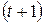 – номера відповідно поточної і наступної ітерацій;
– номера відповідно поточної і наступної ітерацій;
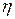 – коефіцієнт швидкості навчання, 0<
– коефіцієнт швидкості навчання, 0< 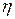 <1;
<1;
i - номер входу;
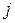 - номер нейрона в шарі.
- номер нейрона в шарі.
Очевидно, що якщо d > Y, то вагові коефіцієнти будуть збільшені і, тим самим, зменшать помилку. Інакше вони будуть зменшені, і Y теж зменшиться, наближаючись до d.
Крок 4. Цикл з кроку 2, поки мережа не перестане помилятися.
На другому кроці на різних ітераціях по черзі у випадковому порядку пред'являються всі можливі вхідні вектори. На жаль, не можна наперед визначити число ітерацій, які потрібно виконати, а в деяких випадках і гарантувати повний успіх.
Збіжність розглянутої процедури встановлюється теоремами, стверджуючими, що для будь-якої класифікації навчальної послідовності можна підібрати такий набір (з нескінченного набору) елементарних нейронів, у якому буде здійснено розділення навчальної послідовності за допомогою лінійного вирішального правила, і що, як відносно задуманої класифікації можна знайти набір елементів, в якому існує рішення, то в рамках цього набору воно буде досягнуте в кінцевий проміжок часу.
Контрольні питання
1. Наведіть структуру персептронного нейрона.
2. Наведіть структуру персептрона з багатьма виходами.
3. Поясніть проблему “ВИКЛЮЧНОГО АБО”
4. Наведіть алгоритм навчання персептрона.
Дата добавления: 2015-10-13; просмотров: 2043;
