Ефективність функціонування нейронних мереж

Ефективність функціонування нейронних мереж встановлюється теоремою про повноту. У 1989 р. Funahashi показав, що нескінченно велика нейронна мережа з єдиним прихованим шаром здатна апроксимувати будь-яку безперервну функцію, сформулювавши дане твердження у формі наступної теореми.

Теорема. Нехай ф(x) - непостійна, обмежена і монотонно зростаюча безперервна функція. Нехай, далі, 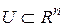– обмежена множиною і 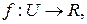– речова безперервна функція, визначена на U.

Тоді для довільного 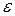>0 існує ціле L і константи W_i, W_ij такі, що апроксимація:

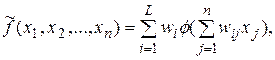(13.1)

задовольняє нерівності:

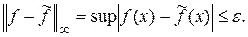(13.2)

Іншими словами, будь-яке безперервне відображення може бути апроксимоване в значенні однорідної топології нейронною мережею з активаційними функціями ф(x) для нейронів прихованого шару і лінійними активаційними функціями для нейронів вихідного шару. На рисунку 13.1 представлена НМ Funahashi для апроксимації скалярної функції векторного аргумента.

Відзначимо, що приведена теорема про повноту є далеко не єдиною з відомих.

Дослідниками доведено, що основними недоліками апарату нейронних мереж являються:

- відсутність строгої теорії щодо вибору структури НМ;

- практична неможливість отримання набутих знань із навченої НМ (нейронна мережа практично завжди – «річ в собі», чорний ящик для дослідника).

Рис. 13.1. Нейронна мережа Funahashi

Контрольні питання

1. Сформулюйте теорему про повноту Funahashi.

2. Наведіть архітектуру НМ Funahashi.

3. Наведіть узагальнені недоліки нейронних мереж.