Використання нейромереж
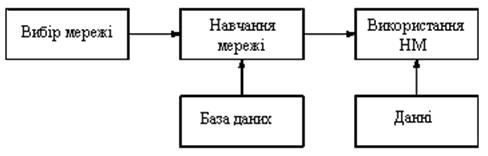 |
Після того, як мережа навчена, ми можемо застосовувати її для вирішення різних задач (рис. 6.1).
Рис. 6.1. Етапи нейромережевого проекту
Найважливіша особливість людського мозку полягає в тому, що, одного разу навчившись певному процесу, він може вірно діяти і в тих ситуаціях, в яких він не бував у процесі навчання.
Наприклад, ми можемо читати майже будь-який почерк, навіть якщо бачимо його перший раз в житті. Так само і нейромережа, грамотним чином навчена, може з великою вірогідністю правильно реагувати на нові, не пред'явлені їй раніше дані. Наприклад, ми можемо намалювати букву «А» іншим почерком, а потім запропонувати нашій мережі класифікувати нове зображення.
Вага навченої мережі береже достатньо багато інформації про схожість і відмінності букв, тому можна розраховувати на правильну відповідь і для нового варіанту зображення.
6.1. Класифікація. Відзначимо, що задачі класифікації (типу розпізнавання букв) дуже погано алгоритмізуються. Якщо у разі розпізнавання букв вірна відповідь очевидна для нас наперед, то в складніших практичних задачах навчена нейромережа виступає як експерт, що володіє великим досвідом і здатний дати відповідь на важке питання.
Прикладом такої задачі служить медична діагностика, де мережа може враховувати велику кількість числових параметрів (енцефалограма, тиск, вага і т.д.). Звичайно, «думку» мережі в цьому випадку не можна вважати остаточною.
Класифікація підприємств за ступенем їх перспективності – це вже звичний спосіб використовування нейромереж у практиці західних компаній (розподіл компаній на перспективні і збиткові). При цьому мережа також використовує безліч економічних показників, складним чином зв'язаних між собою.
Нейромережевий підхід особливо ефективний у задачах експертної оцінки по тій причині, що він поєднує в собі здібність комп'ютера до обробки чисел і здатність мозку до узагальнення і розпізнавання. Говорять, що у хорошого лікаря здібність до розпізнавання у своїй області така велика, що він може провести приблизну діагностику вже за зовнішнім виглядом пацієнта.
Можна погодитися також, з тим що досвідчений трейдер відчуває направлення руху ринку за видом графіка. Проте в першому випадку всі чинники наочні, тобто характеристики пацієнта миттєво сприймаються мозком як «бліде обличчя», «блиск в очах» і т.д. У другому ж випадку враховується тільки один чинник, показаний на графіку – курс за певний період часу. Нейромережа дозволяє обробляти величезну кількість чинників (до декількох тисяч), незалежно від їх наочності – це універсальний «хороший лікар», який може поставити свій діагноз в будь-якій області.
6.2. Кластеризація і пошук залежності. Крім задач класифікації, нейромережі широко використовуються для пошуку залежності в даних і кластеризації.
Наприклад, нейромережа на основі методики МГОА (метод групового обліку аргументів) дозволяє на основі навчальної вибірки побудувати залежність одного параметра від інших у вигляді полінома. Така мережа може не тільки миттєво вивчити таблицю множення, але і знайти складну приховану залежність в даних (наприклад, фінансових), які не виявляються стандартними статистичними методами.
Кластеризація – це розбиття набору прикладів на декілька компактних областей (кластерів), причому число кластерів наперед невідоме. Кластеризація дозволяє представити неоднорідні дані в більш наочному вигляді і використати далі для дослідження кожного кластера різними методами. Наприклад, таким чином можна швидко виявити фальсифіковані страхові випадки або нечесні підприємства.
6.3. Прогнозування. Задачі прогнозування особливо важливі для практики, зокрема, для фінансових пропозицій, тому пояснимо способи вживання нейромереж в цій області більш детально.
Розглянемо практичну задачу, відповідь в якій невідома – задачу прогнозування курсу акцій на 1 день вперед.
Нехай у нас є база даних, що містить значення курсу за останні 300 днів. Найпростіший варіант у даному випадку – спробувати побудувати прогноз завтрашньої ціни на основі курсів за останні декілька днів. Зрозуміло, що прогнозуюча мережа повинна мати всього один вихід і стільки входів, скільки попередніх значень ми хочемо використовувати для прогнозу – наприклад, 4 останніх значення. Скласти навчальний приклад дуже просто: вхідними значеннями будуть курси за 4 останніх днів, а бажаним виходом – відомий нам курс на наступний день за цими чотирма, тобто кожний рядок таблиці з навчальною послідовністю (вибіркою) є навчальним прикладом, де перші 4 числа – вхідні значення мережі, а п'яте число – бажане значення виходу.
Зазначимо, що об'єм навчальної вибірки залежить від вибраної кількості входів. Якщо зробити 299 входів, то така мережа потенційно могла б будувати кращий прогноз, ніж мережа з 4 входами, проте у цьому випадку ми маємо справу з величезним масивом даних, що робить навчання і використовування мережі практично неможливим. При виборі числа входів слід враховувати це, вибираючи розумний компроміс між глибиною прогнозу (число входів) і якістю навчання (об'єм тренувального набору).
Взагалі кажучи, залежно від типу вирішуваної задачі, доцільно застосовувати нейронну мережу найбільш підходящу для такої задачі структури.
Контрольні питання
1. Наведіть етапи нейромережевого проекту.
2. Використання НМ для класифікації? Приклади?
3. Використання НМ для кластеризації і пошуку залежності? Приклади?
4. Використання НМ для прогнозування? Приклади?
Дата добавления: 2015-10-13; просмотров: 1344;
