Навчання нейронних мереж

Навчити нейромережу – значить, повідомити їй, про те чого ми від неї очікуємо. Цей процес дуже схожий на навчання дитини алфавіту. Показавши дитині зображення букви «А», ми питаємо його: «яка це буква?» Якщо відповідь невірна, ми повідомляємо дитині ту відповідь, яку ми хотіли б від неї одержати: «це буква А».

Дитина запам'ятовує цей приклад разом з вірною відповіддю, тобто в її пам'яті відбуваються деякі зміни в потрібному напрамку. Ми повторюватимемо процес пред'явлення букв знову і знову доти, коли всі букви твердо запам'ятають. Такий процес називають «навчання з вчителем» (рис. 5.1).

При навчанні мереж ми діємо абсолютно аналогічно. У нас є деяка база даних, що містить приклади (набір рукописних зображень букв).

Демонструючи зображення букви «А» на вхід мережі, ми одержуємо від неї деяку відповідь, не обов’язково вірну. Нам відома і вірна (бажана) відповідь – у даному випадку нам хотілося б, щоб на виході з міткою «А» рівень сигналу був максимальний. Звичайно як бажаний вихід у задачі класифікації беруть набір (1, 0, 0,...), де 1 стоїть на виході з міткою «А», а 0 – на всій решті виходів.

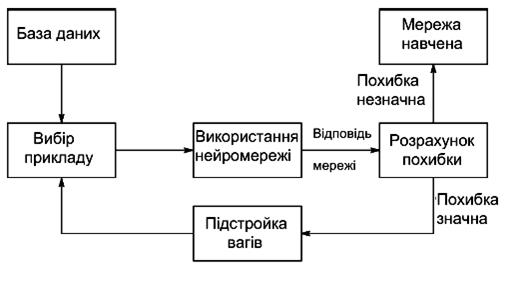
Рис. 5.1. Ілюстрація процесу навчання НМ

Вирахувавши різницю між бажаною відповіддю і реальною відповіддю мережі, ми одержуємо 33 числа – вектор помилки.

Алгоритм навчання – це набір формул, який дозволяє по вектору помилки обчислити необхідні поправки для ваг мережі.

Одну і ту ж букву (а також різні зображення однієї і тієї ж букви) ми можемо пред'являти мережі багато разів. У цьому значенні навчання швидше нагадує повторення вправ у спорті – тренування.

Виявляється, що після багатократного пред'явлення прикладів вага мережі стабілізується, причому мережа дає правильні відповіді на всі (або майже всі) приклади з бази даних. У такому разі говорять, що «мережа вивчила всі приклади», «мережа навчена», або «мережа натренована». У програмних реалізаціях можна бачити, що у процесі навчання функція помилки (наприклад, сума квадратів помилок по всім виходах) поступово зменшується. Коли функція помилки досягає нуля або прийнятного малого рівня, вправи зупиняють, а одержану мережу вважають натренованою і готовою до використання на нових даних.

Важливо відзначити, що вся інформація, яку мережа має про задачу, міститься в наборі прикладів. Тому якість навчання мережі напряму залежить від кількості прикладів у навчальній вибірці, а також від того, наскільки повно ці приклади описують дану задачу. Так, наприклад, безглуздо використовувати мережу для прогнозу фінансової кризи, якщо в навчальній вибірці кризи не представлено. Вважається, що для повноцінного тренування потрібні хоча б декілька десятків (а краще сотень) прикладів.

Математично процес навчання можна описати таким чином.

У процесі функціонування нейронна мережа формує вихідний сигнал Y відповідно до вхідного сигналу X, реалізовуючи деяку функцію Y = G(X). Якщо архітектура мережі задана, то вид функції G визначається значеннями синаптичних вагів і зсувів мережі.

Нехай рішенням деякої задачі є функція Y =F(X), задана парами вхідних-вихідних даних (X¹, У¹ ), (X², У² ) ,..., (X^N, Y^N), для яких У^k = F(X^k) (k = 1, 2,..., N).

Навчання полягає у пошуці (синтезі) функції G, близької до F у значенні деякої функції помилки Е (рис. 5.1).

Якщо вибрані множини навчальних прикладів – пара (X^k, У^k) (де k=1,2,..., N) і спосіб обчислення функції помилки Е, то навчання нейронної мережі перетворюється на задачу багатовимірної оптимізації, що має дуже велику розмірність, при цьому, оскільки функція Е може мати довільний вигляд, навчання у загальному випадку – багатоекстремальна неопукла задача оптимізації.

Для вирішення цієї задачі можуть бути використані наступні (ітераційні) алгоритми:

- алгоритми локальної оптимізації з обчисленням часткових похідних першого порядку;

- алгоритми локальної оптимізації з обчисленням часткових похідних першого і другого порядку;

- стохастичні алгоритми оптимізації;

- алгоритми глобальної оптимізації.

До першої групи відносяться: градієнтний алгоритм (метод найшвидшого спуску); методи з одновимірною і двовимірною оптимізацією цільової функції у напрямі антиградієнта; метод зв’язаних градієнтів; методи, що враховують напрям антиградієнта на декількох кроках алгоритму.

До другої групи відносяться: метод Ньютона, квазіньютонівські методи, метод Гауса-Ньютона, метод Льовенберга-Марквардта і інші.

Стохастичними методами є: пошук у випадковому направленні, імітація відпалу, метод Монте-Карло (чисельний метод статистичних випробувань).

Задачі глобальної оптимізації розв'язуються за допомогою перебору значень змінних, від яких залежить цільова функція (функція помилки Е).

5.1. Алгоритм зворотного розповсюдження помилки. Розглянемо ідею одного з найпоширеніших алгоритмів навчання – алгоритм зворотного розповсюдження помилки (back propagation). Це ітеративний градієнтний алгоритм навчання, який використовується з метою мінімізації середньоквадратичного відхилення поточного виходу і бажаного виходу багатошарових нейронних мереж.

Алгоритм зворотного розповсюдження використовується для навчання багатошарових нейронних мереж з послідовними зв’язками. Як зазначено вище, нейрони в таких мережах діляться на групи із загальним вхідним сигналом – шари, при цьому на кожний нейрон першого шару подаються всі елементи зовнішнього вхідного сигналу, а всі виходи нейронів того шару подаються на кожний нейрон шару (q+1). Нейрони виконують зважене (з синаптичними вагами) підсумовування елементів вхідних сигналів; до даної суми додається зсув нейрона. Над отриманим результатом виконується активаційною функцією нелінійне перетворення. Значення функції активації є вихід нейрона.

У багатошарових мережах оптимальні вихідні значення нейронів всіх шарів, окрім останнього, як правило, невідомі, і трьох- або більш шаровий персептрон вже неможливо навчити, керуючись тільки величинами помилок на виходах НМ. Найбільш прийнятним варіантом навчання в таких умовах виявився градієнтний метод пошуку мінімуму функції помилки з розглядом сигналів помилки від виходів НМ до її входів, в напрямку, зворотному прямому розповсюдженню сигналів у звичайному режимі роботи. Цей алгоритм навчання НМ одержав назву процедури зворотного розповсюдження.

У такому алгоритмі функція помилки є сумою квадратів помилки мережі бажаного виходу і реального. При обчисленні елементів вектора-градієнта був використаний своєрідний вид похідних функцій активації сигмоїдального типу. Алгоритм діє циклічно (ітеративно), і його цикли прийнято називати епохами. На кожній епосі на вхід мережі по черзі подаються всі навчальні спостереження, вихідні значення мережі порівнюються з цільовими значеннями і вираховується помилка. Значення помилки, а також градієнта поверхні помилок використовується для корегування вагів, після чого всі дії повторюються. Початкова конфігурація мережі обирається випадковим чином, і процес навчання припиняється коли пройдена певна кількість епох, або коли помилка досягне деякого певного рівня малості, або коли помилка перестане зменшуватися (користувач може сам вибрати потрібну умову зупинки).

Приведемо мовний опис алгоритму.

Крок 1. Вагам мережі присвоюються невеликі початкові значення.

Крок 2. Вибирається чергова навчальна пара (X, Y); вектор X подається на вхід мережі.

Крок 3. Обчислюється вихід мережі.

Крок 4. Обчислюється різниця між виходом мережі, що вимагається (цільовим, Y) і реальним (обчисленим).

Крок 5. Вага мережі корегується так, щоб мінімізувати помилку.

Крок 6. Кроки з 2-го по 5-й повторюються для кожної пари навчальної множини до тих пір, поки помилка на всій множині не досягне прийнятної величини.

Кроки 2 і 3 подібні тим, які виконуються у вже навченій мережі.

Обчислення у мережі виконуються пошарово. На кроці 3 кожний з виходів мережі віднімається з відповідної компоненти цільового вектора з метою отримання помилки. Ця помилка використовується на кроці 5 для корекції вагів мережі.

Кроки 2 і 3 можна розглядати як «прохід вперед», оскільки сигнал розповсюджується по мережі від входу до виходу. Кроки 4 і 5 складають «зворотний прохід», оскільки тут обчислюваний сигнал помилки розповсюджується назад по мережі і використовується для підстроювання вагів.

Математичне представлення алгоритму розглянемо спочатку на прикладі найпростішої нейронної мережі, що містить тільки один нейрон (умовно позначений колом (рис. 5.2).

Вважатимемо, що вихід (output) мережі о = f(net) визначається функцією активації сигмоїдного типу.

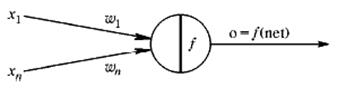
Рис. 5.2. НМ із одного нейрона

Припустимо, що для навчання мережі використовується вибірка:

x¹ = (x₁¹, x₂¹, …, x_n¹)^T, y¹,

x² = (x₁², x₂², …, x_n²)^T, y²,

……………………………..

X^N = (x₁^N, x₂^N, …, x_n^N)^T, y^N.

де: у^k – значення бажаного (цільового) виходу.

Як функція помилки для k-го зразка (k-го елемента навчальної вибірки) приймемо величину, пропорційну квадрату різниці бажаного виходу і виходу мережі:

(5.1)

Відповідно, сумарна функція помилки по всіх елементах вибірки:

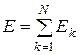(5.2)

Очевидно, як E_k, так і E є функціями вектора вагів мережі w. Задача навчання мережі зводиться у даному випадку до підбору такого вектора w, при якому досягається мінімум E. Таку задачу оптимізації вирішуватимемо градієнтним методом, використовуючи співвідношення:

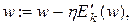(5.3)

де: « : = » – оператор присвоєння,

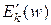– апозначення вектора-градієнта,

– деяка константа.

Представляючи вектор у розгорненому вигляді для похідної сигмоїдної функції, одержимо:

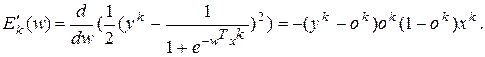(5.4)

Це дає можливість записати алгоритм корекції (підстроювання) вектора вагових коефіцієнтів мережі у формі:

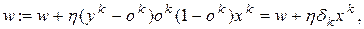(5.5)

де:

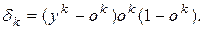(5.6)

Одержані математичні вирази повністю визначають алгоритм навчання даної НМ, який може бути представленний тепер у наступному вигляді.

1.Задаються деякі (0< <1), Е_max і деяка мала випадкова вага мережі.

2.Задаються k=1 і Е=0.

3.Вводиться чергова навчальна пара (x^k, у^k ).

Проводяться позначення

x := x^k, у := у^k

обчислюється величина виходу мережі:

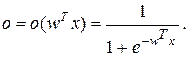(5.7)

4.Обновляється (корегується) вага:

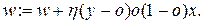(5.8)

5. Корегується (нарощується) значення функції помилки:

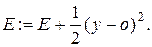(5.9)

6. Якщо k < N, тоді k := k+1 і перехід до кроку 3, у протилежному випадку – перехід до кроку 7.

7. Завершення циклу навчання. Якщо Е<Е_max, то закінчення всієї процедури навчання. Якщо Е 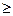E_max, тоді починається новий цикл навчання переходом до кроку 2.

Розглянемо тепер більш загальний випадок, вважаючи, що двошарова НМ містить декілька (L) прихованих нейронів і один вихідний (рис. 5.3).

У даному випадку функція помилки залежить від векторів вагів прихованого шару і вектора вагів, пов'язаних з вихідним нейроном. Вихід мережі описується виразом:

(5.10)

де: W – вектор вагів вихідного нейрона,

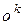– вектор виходів нейронів прихованого шару з елементами.

Рис. 5.2. Двошарова нейронна мережа

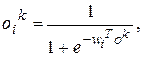(5.11)

де: w_i – вектор вагів, пов'язаних з i-м прихованим нейроном, i=1,2,…,L.

Правило коректування вагів у даній НМ також засновано на мінімізації квадратичної функції помилки градієнтним методом на основі виразів:

(5.12)

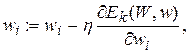(5.13)

де: =const – коефіцієнт швидкості навчання (0 < < 1), i=1,2,…,L.

Використовуючи правило диференціювання складної функції і вираз для похідної сигмоїдної функції активації, отримаємо:

(5.14)

звідки слідує:

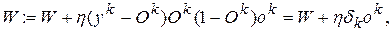(5.15)

або в скалярній формі:

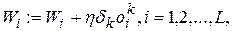(5.16)

де:

(5.17)

Поступаючи аналогічно, знайдемо:

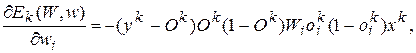(5.18)

звідки одержуємо:

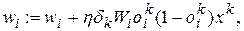(5.19)

або (в скалярній формі):

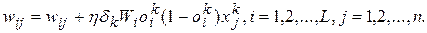(5.20)

Алгоритм навчання може бути тепер представлений у вигляді слідуючих кроків:

1.Задаються деякі (0< 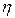<1), Е_max і деяка мала випадкова вага 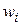мережі.

2.Задаються k =1 і Е=0.

3.Вводиться чергова навчальна пара (x^k, у^k). Вводяться позначення:

(5.21)

і обчислюється величина виходу мережі:

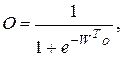(5.22)

де: W – вектор вагів вихідного нейрона, о^k – вектор виходів нейронів прихованого шару з елементами:

(5.23)

w_i позначає вектор вагів, пов'язаних з i-м прихованим нейроном, i=1,2,...,L.

4.Проводиться коректування терезів вихідного нейрона:

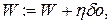(5.24)

де:

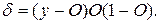(5.25)

5.Коректується вага нейронів прихованого шару:

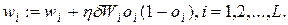(5.26)

6.Коректується (нарощується) значення функції помилки:

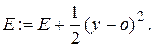(5.27)

Якщо k<N, тоді k:=k+1 і перехід до кроку 3, у протилежному випадку перехід на крок 8.

7. Завершення циклу навчання. Якщо Е<Е_max, то закінчення всієї процедури навчання. Якщо Е 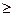Е_max, тоді починається новий цикл навчання з переходом до кроку 2.

Розглянута процедура може бути легко узагальнена на випадок мережі з довільною кількістю шарів і нейронів в кожному шарі.

Звернемо увагу, на те що в даній процедурі спочатку відбувається корекція вагів для вихідного нейрона, а потім – для нейронів прихованого шару, тобто від кінця мережі до її початку. Звідси і назва – зворотне розповсюдження помилки. Зважаючи на використання для позначень грецької букви 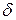, цю процедуру навчання називають ще іноді узагальненим дельта-правилом.

Дамо висловленому геометричну інтерпретацію.

У алгоритмі зворотного розповсюдження обчислюється вектор градієнта поверхні помилок. Цей вектор вказує напрямок найкоротшого спуску по поверхні з даної точки, тому, якщо ми «трохи» просунемося по ньому, помилка зменшиться. Послідовність таких кроків (сповільнююча по мірі наближення до дна) врешті-решт приведе до мінімуму того або іншого типу. Певну складність тут представляє питання про те, яку потрібно брати довжину кроків (що визначається величиною коефіцієнта швидкості навчання ).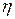

При великій довжині кроку збіжність буде більш швидкою, але є небезпека перестрибнути через рішення або (якщо поверхня помилок має особливо складну форму) піти у неправильному напрямі.

Класичним прикладом такого явища при навчанні нейронної мережі є ситуація, коли алгоритм дуже повільно просувається по вузькому яру з крутими схилами, стрибаючи з однієї його сторони на іншу. Навпаки, при маленькому кроці, ймовірно, буде схоплений вірний напрям, проте при цьому буде потрібно дуже багато ітерацій.

На практиці величина кроку береться пропорційній крутизні схилу (отже алгоритм уповільнює хід поблизу мінімуму) з деякою константою ( 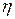), яка, як наголошувалося, називається коефіцієнтом швидкості навчання. Правильний вибір швидкості навчання залежить від конкретної задачі і звичайно здійснюється дослідним шляхом; ця константа може також залежати від часу, зменшуючись у міру просування алгоритму.

Звичайно алгоритм видозмінюється так, щоб включати доданок імпульсу (або інерції). Цей член сприяє просуванню у фіксованому напрямі, тому якщо було зроблено декілька кроків в одному і тому ж напрямі, то алгоритм «збільшує швидкість», що (іноді) дозволяє уникнути локального мінімуму, а також швидше проходити плоскі ділянки.

Таким чином, алгоритм діє ітеративно, і його кроки прийнято називати епохами. На кожній епосі на вхід мережі почерзі подаються всі навчальні спостереження, вихідні значення мережі порівнюються з цільовими значеннями і обчислюється помилка. Значення помилки, а також градієнта поверхні помилки використовується для корегування вагів, після чого всі дії повторюються. Початкова конфігурація мережі вибирається випадковим чином, і процес навчання припиняється, або коли пройдена певна кількість епох, або коли помилка досягне деякого певного рівня малості, або коли помилка перипиняє зменшуватися (користувач може сам обрати потрібну умову зупинки).

Класичний метод зворотного розповсюдження відноситься до алгоритмів з лінійною збіжністю і відомими недоліками його є: невисока швидкість збіжності (велике число необхідних ітерацій для досягнення мінімуму функції помилки), можливість сходитися не до глобального, а до локальних рішень (локальним мінімумам відзначеної функції), можливість паралічу мережі (при якому більшість нейронів функціонує при дуже великих значеннях аргументу функцій активації, тобто на її пологій ділянці; оскільки помилка пропорційна похідній, яка на даних ділянках мала, то процес навчання практично завмирає).

Для усунення цих недоліків були запропоновані численні модифікації алгоритму зворотного розповсюдження, які зв'язані з використанням різних функцій помилки, різних процедур визначення напряму і величини кроку і т.ін.

5.2. Перенавчання і узагальнення. Одна з найбільш серйозних труднощів висловленого підходу полягає у тому, що таким чином ми мінімізуємо не ту помилку, яку насправі потрібно мінімізувати – помилку, яку можна чекати від мережі, коли їй подаватимуться абсолютно нові спостереження.

Інакше кажучи, ми хотіли б, щоб нейронна мережа мала здатність узагальнювати результат на нові спостереження. У дійсності мережа навчається мінімізувати помилку на досліджуваній множині, і при відсутності ідеальної і нескінченно великої навчальної множини це зовсім не те ж саме, що мінімізувати «справжню» помилку на поверхні помилок у наперед невідомій моделі явища.

Сильніше за все ця відмінність виявляється у проблемі перенавчання, або дуже близької підгонки. Це явище буде простіше продемонструвати не для нейронної мережі, а на прикладі апроксимації за допомогою поліномів – при цьому суть явища абсолютно така ж сама.

Поліном (або многочлен) – це вираз, що містить тільки константи і цілі ступені незалежної змінної.

Приклади: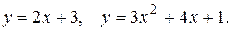

Графіки поліномів можуть мати різну форму, причому чим вище ступінь многочлена (і, тим самим, чим більше членів в нього входить), тим більш складною може бути ця форма. Якщо у нас є деякі дані, ми можемо поставити мету підігнати до них поліномінальну криву (модель) і одержати таким чином пояснення для даної залежності. Наші дані можуть бути зашумлені, тому не можна вважати, що найкраща модель задається кривою, яка в точності проходить через всі наявні точки. Поліном низького порядку може бути недостатньо гнучким засобом для апроксимації даних, тоді як поліном високого порядку може виявитися занадто гнучким, і точно слідуватиме даним, приймаючи при цьому складну форму, що не має ніякого відношення до форми справжньої залежності.

Нейронна мережа стикається з точно такою ж трудністю. Мережі з великим числом вагів моделюють складніші функції і, отже, схильні до перенавчання. Мережа ж з невеликою кількістю вагів може виявитися недостатньо гнучкої, щоб змоделювати наявну залежність.

Як же вибрати «правильний» ступінь складності для мережі? Майже завжди складніша мережа дає меншу помилку, але це може свідчити не про хорошу якість моделі, а про перенавчання.

Відповідь полягає в тому, щоб використовувати механізм контрольної крос-перевірки, при якій частина навчальних спостережень резервується і в навчанні по алгоритму зворотного розповсюдження не використовується. Натомість, по мірі роботи алгоритму, вона використовується для незалежного контролю результату.

На самому початку роботи помилки мережі на навчальній і контрольній множинах будуть однаковими (якщо вони істотно відрізняються, то, ймовірно, розбиття всіх прикладів на дві множини було неоднорідне). У міру того як мережа навчається, помилки навчання, поволі зменшуються, і поки навчання зменшує дійсну функцію помилок, помилка на контрольній множині також буде зменшуватись. Якщо ж контрольна помилка перестала зменшуватись або навіть стала зростати, це вказує на те, що мережа почала дуже близько апроксимувати дані і навчання слід зупинити. Це явище занадто точної апроксимації у процесі навчання і називається перенавчанням. Якщо таке трапилося, то звичайно радять зменшити число прихованих елементів або шарів, бо мережа є дуже потужною для даної задачі. Якщо ж мережа, навпаки, була взята недостатньо складна для того, щоб моделювати дану залежність, то перенавчання, швидше за все, не відбудеться, і обидві помилки – навчання і перевірки – не досягнуть достатнього рівня малості.

Описані проблеми з локальними мінімумами і вибором розміру мережі призводять до того, що при практичній роботі з нейронними мережами, як правило, доводиться експериментувати з великою кількістю різних мереж, деколи навчаючи кожну з них по кілька разів (щоб не бути введеним в оману локальними мінімумами) і порівнювати одержані результати. Головним показником якості результату є контрольна помилка. При цьому відповідно до загальнонаукового принципу, згідно якому при інших рівних слід віддати перевагу більш простій моделі, з двох мереж з приблизно рівними помилками контролю має сенс вибрати ту, яка менше.

Класичний метод зворотного розповсюдження відноситься до алгоритмів з лінійною збіжністю. Для збільшення швидкості збіжності необхідно використовувати матриці других похідних функції помилки.

Були запропоновані численні модифікації алгоритму зворотного розповсюдження, які зв'язані з використанням різних функцій помилки, різних процедур визначення напряму і величини кроку.

1. Функції помилки:

- інтегральні функцій помилки на всій сукупності навчальних прикладів;

- функції помилки цілих і дробових ступенів.

2. Процедури визначення величини кроку на кожній ітерації:

- дихотомія;

- інерційні співвідношення;

- відпал.

3. Процедури визначення напряму кроку:

- з використанням матриці похідних другого;

- з використанням напрямів на декількох кроках.

5.3. Навчання без вчителя. Розглянутий алгоритм навчання нейронної мережі за допомогою процедури зворотного розповсюдження має на увазі наявність якоїсь зовнішньої ланки, надаючи мережі окрім вхідних також і цільові вихідні образи. Алгоритми, що користуються подібною концепцією, називаються алгоритмами навчання з вчителем. Для їх успішного функціонування необхідна наявність експертів, що створюють на попередньому етапі для кожного вхідного образу еталонний вихідний. Оскільки створення штучного інтелекту рухається по шляху копіювання природних прообразів, учені не припиняють суперечку на тему, чи можна рахувати алгоритми навчання з вчителем натуральными або ж вони повністю штучні. Наприклад, навчання людського мозку, на перший погляд, відбувається без вчителя: на зорові, слухові, тактильні і інші рецептори поступає інформація ззовні, і усередині нервової системи відбувається самоорганізація. Проте не можна заперечувати і того, що в житті людини не мало вчителів – і в прямому, і в переносному значеннях – які координують зовнішні дії. Разом з тим, чим би не закінчилася суперечка прихильників цих двох концепцій навчання – з вчителем і без вчителя, вони обидві мають право на існування.

Головне, що робить навчання без вчителя привабливим – це його «самостійність». Процес навчання, як і у разі навчання з вчителем, полягає в підстроюванні вагів мережі. Деякі алгоритми, правда, змінюють і структуру мережі, тобто кількість нейронів і їх взаємозв'язкок, але такі перетворення правильніше назвати більш широким терміном – самоорганізації, але тут вони розглядатися не будуть.

Очевидно, що підстроювання вагів може проводитися тільки на підставі інформації, доступної у нейроні, тобто його стану і вже наявних вагових коефіцієнтів. Виходячи з цього міркування, по аналогії з відомими принципами самоорганізації нервових клітин, побудовані алгоритми навчання Хебба.

Сигнальний метод навчання Хебба полягає в зміні вагів за наступним правилом:

(5.28)

де: 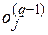– вихідне значення j-гo нейрона шару (q-1),

– вихідне значення і-гo нейрона шару q;

w_ij – ваговий коефіціент синапсу, що сполучає ці нейрони,

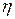– коефіцієнт швидкості навчання.

Надалі, для спільності, під q мається на увазі довільний шар мережі. При навчанні по даному методу посилюються зв'язки між збудженими нейронами.

Повний алгоритм навчання із застосуванням вищенаведеної формули виглядатиме так:

1. На стадії ініціалізації всім ваговим коефіцієнтам присвоюються невеликі випадкові значення.

2. На входи мережі подається вхідний образ, і сигнали збудження розповсюджуються по всіх шарах згідно принципам класичних мереж прямого розповсюдження (feedforward), тобто для кожного нейрона розраховується зважена сума його входів, до якої потім застосовується активаційна (передавальна) функція нейрона, внаслідок чого встановлюється його вихідне значення.

3. На підставі набутих вихідних значень нейронів по приведеній формулі проводиться зміна вагових коефіцієнтів.

5.Цикл з кроку 2, поки вихідні значення мережі не зафіксуються із заданою точністю.

6.Вживання цього нового способу визначення завершення навчання, відмінного від використованого для мережі зворотного розповсюдження, це обумовлено тим, що підстроювані значення синапсів фактично не обмежені.

На другому кроці циклу поперемінно пред'являються всі образи з вхідного набору.

Слід зазначити, що вид відгуків на кожний клас вхідних образів невідомий наперед і буде довільне поєднанням станів нейронів вихідного шару, обумовленим випадковим розподілом вагів на стадії ініціалізації. Разом з тим, мережа здатна узагальнювати схожі образи, відносячи їх до одному класу. Тестування навченої мережі дозволяє визначити топологію класів у вихідному шарі. Для приведення відгуків навченої мережі до зручного уявлення можна доповнити мережу одним шаром, який, наприклад, по алгоритму навчання одношарового персептрона необхідно примусити відображати вихідні реакції мережі в необхідні образи.

Інший алгоритм навчання без вчителя – алгоритм Кохонена (Kohonen) – передбачає самонавчання за правилом «переможець забирає все». Структура мережі, що реалізовує дане правило, представлена на рисунку 5.3.

Критерій підстроювання вагів мережі (всі вектори вагів повинні бути нормалізовані, тобто мати одиничну довжину: ||w_і||=1, і=1,2,...,m) виглядає таким чином:

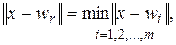(5.29)

Рис. 5.3. Структура мережі Кохонена

де індекс r позначає нейрон-переможець, відповідний вектору вагів w_r, який ближче всіх розташований до (поточному) вхідного вектору x.

Оскільки (з урахуванням того, що ):

(5.30)

процедура знаходження w_r еквівалентна рішення оптимізаційної задачі:

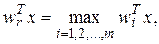(5.31)

можна дати певну геометричну інтерпретацію (рис. 5.4).

Оскільки скалярний добуток 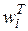з урахуванням ||w_і||=1 представляє собою просто проекцію вектора x на напрям вектора w_і, тоді нейрон-переможець визначається по тому вектору вагів, чий напрям ближче до напряму x (на рис. 5.4 таким є вектор w₂).

Після виявлення нейрона-переможця його вихід встановлюється рівним одиниці (у решти нейронів встановлюються нульові виходи), а вага коректується так, щоб зменшити квадрат величини розузгодження ||x-w_r||². При використанні градієнтного підходу це приводить до наступного математичного формулювання:

(5.32)

де: 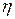- константа, яка визначає швидкість навчання.

Рис. 5.4. Ілюстрація до алгоритму самонавчання Кохонена

Знайдемо похідну в правій частині останнього виразу:

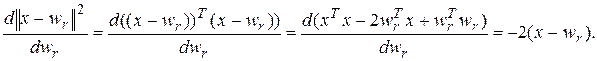(5.33)

При цьому:

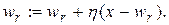(5.34)

Cлід зазначити, що корекції вагів у інших нейронів не проводяться.

Алгоритм навчання (без вчителя) Кохонена може бути тепер описаний таким чином.

1.Задаються випадкові нормалізовані по довжині вектори w_i.

2.Початок циклу навчання; введення чергового вектора входів x.

3.Визначення нейрона-переможця, коректування вектора його вагів і задання одиничного виходу:

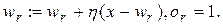(5.35)

4.Нормалізація знайденого вектора:

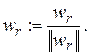(5.36)

5. Задання значень для решти нейронів:

(5.37)

6. Перевірка виконання правила зупинки (у якості такого правила можна прийняти, наприклад, стабілізацію векторів вагів на якихось значеннях); якщо воно не виконано – продовження циклу навчання (переходом до кроку 2), в протилежному випадку – перехід до кроку 7.

7. Кінець процедури навчання.

Очевидно, що вираз для корекції вектора вагових коефіцієнтів нейрона-переможця може бути представлений у формі:

(5.38)

тобто нове (скоректоване) значення даного вектора являється зваженою сумою старого значення (до корекції) і пред’явленого вектора входів (рис. 5.5).

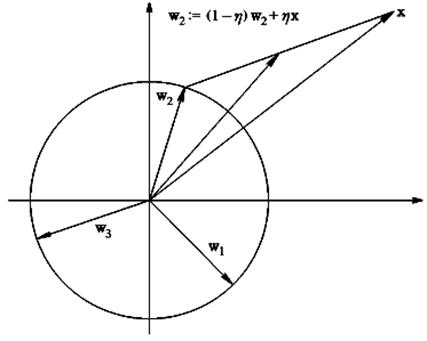
Рис. 5.5. Ілюстрація до процедури корекції вектора вагів нейрона-переможця

Неважко показати, що підсумковим результатом подібних корекцій (в умовах даного прикладу для двовимірного випадку) є вектори вагів, що показують на центри кластерів (центри групування) вхідних образів (рис. 5.6).

Інакше кажучи, алгоритм навчання Кохонена забезпечує рішення задачі автоматичної класифікації, тобто віднесення вектора входів, до одного з класів (на рис. 5.6 таких класів 3).

Правда, така класифікація можлива тільки у разі, коли кластери є лінійно роздільними (гіперплощинами) щодо початку координат в просторі входів НМ.

Відзначимо, що число нейронів НМ для успішного вирішення вказаної задачі повинне бути не менше ніж число кластерів; оскільки точне число кластерів може бути наперед невідоме, кількість нейронів задають з певним запасом.

«Зайві» нейрони, у яких в процесі навчання мережі ваги змінюються хаотично після закінчення даного процесу можуть бути видалені.

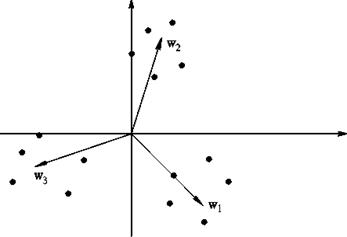
Рис. 5.6. Вектори вагів НМ після закінчення процесу навчання

Контрольні питання

1. Пояснити значення терміну “навчання” НМ.

2. Навести узагальнений алгоритм процесу навчання НМ.

3. Пояснити суть алгоритму навчання НМ зворотного розповсюдження помилки.

4. Поясніть значення термінів “перенавчання” та “узагальнення” НМ.

5. Пояснити алгоритм навчання НМ без учителя.