Топологія нейронних мереж

З погляду топології, серед нейронних мереж, сформованих на основі нейроподібних елементів, можна виділити три основні типи: повнозв'язні мережі (рис. 4.1а); багатошарові мережі (рис. 4.1б); слабозв’язні мережі (нейронні мережі з локальними зв'язками) (рис. 4.1в).

Повнозв'язні мережі представляють собою ШНМ, кожний нейрон якої передає свій вихідний сигнал решті нейронів, у тому числі і самому собі. Всі вхідні сигнали подаються всім нейронам. Вихідними сигналами мережі можуть бути всі або деякі вихідні сигнали нейронів після декількох тактів функціонування мережі.

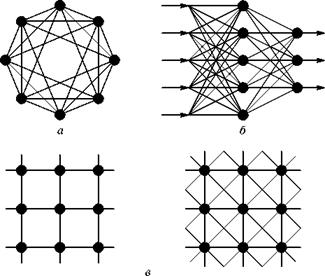
Рис. 4.1. Архітектура нейронних мереж

У багатошарових мережах нейрони об'єднуються в шари. Шар містить сукупність нейронів з єдиними вхідними сигналами. Число нейронів в кожному шарі може бути будь-ким і ніяк наперед не пов'язане з кількістю нейронів в інших шарах. У загальному випадку мережа складається з Q шарів, пронумерованих зліва направо. Зовнішні вхідні сигнали подаються на входи нейронів першого шару (вхідний шар часто нумерують як нульовий), а виходами мережі є вихідні сигнали останнього шару. Вхід нейронної мережі можна розглядати як вихід «нульового шару» вирождених нейронів, які служать лише як розподільчі пункти, підсумовування і перетворення сигналів тут не проводиться. Окрім вхідного і вихідного шарів в багатошаровій нейронній мережі є один або декілька проміжних (прихованих) шарів. Зв'язки від виходів нейронів деякого шару q до входів нейронів наступного шару (q + +1) називаються послідовними.

У свою чергу, серед багатошарових мереж виділяють наступні типи.

1. Монотонні. Це спеціальний окремий випадок мереж з додатковими умовами на зв'язки і елементи. Кожний шар, окрім останнього (вихідного), розбитий на два блоки: збурення (В) і гальмівний (Т). Зв'язки між блоками теж розділяються на гальмівні і збурюючі. Якщо від блоку А до блоку С ведуть тільки збурюючі зв'язки, то це означає, що будь-який вихідний сигнал блоку є монотонною неспадаючою функцією будь-якого вихідного сигналу блоку А. Якщо ж ці зв'язки тільки гальмуючі, то будь-який вихідний сигнал блоку С є незростаючою функцією будь-якого вихідного сигналу блоку А. Для елементів монотонних мереж необхідна монотонна залежність вихідного сигналу елемента від параметрів вхідних сигналів.

2. Мережі без зворотних зв'язків. У таких мережах нейрони вхідного шару одержують вхідні сигнали, перетворють їх і передають нейронам 1-го прихованого шару, далі спрацьовує 1-й прихований шар і т.д. до Q-гo, який видає вихідні сигнали для інтерпретатора і користувача (рис. 4.2). Якщо не обумовлене інше, то кожний вихідний сигнал і-го шару подається на вхід всіх нейронів -го шару; проте можливий варіант з'єднання -го шару з довільним 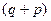-м шаром.

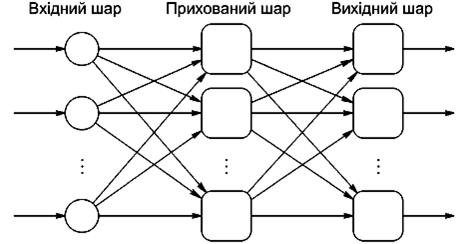
Рис. 4.2. Багатошарова (двошарова) мережа прямого розповсюдження

Слід зазначити, що класичним варіантом таких мереж є мережі прямого розповсюдження (рис. 4.2).

3. Мережі із зворотними зв'язками. Це мережі, у яких інформація з подальших шарів передається на попередні.

Як приклад мереж із зворотними зв'язками на рисунку 4.3 представлені так звані частково-рекурентні мережі Елмана і Жордана.

Відомі мережі можна розділити за принципом структури нейронів в них на гомогенні або однорідні і гетерогенні. Гомогенні мережі складаються з нейронів одного типу з єдиною функцією активації. У гетерогенну мережу входять нейрони з різними функціями активації.

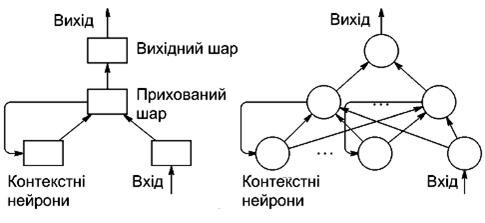
Рис. 4.3. Частково-рекурентні мережі Елмана

Важливо відзначити існування бінарних і аналогових мереж. Перші з них оперують з двійковими сигналами, і вихід кожного нейрона може приймати тільки два значення: логічний нуль («загальмований» стан) або логічна одиниця («збуджений» стан).

Ще одна класифікація ділить НМ на асинхронні і синхронні. У першому випадку в кожний момент часу свій стан змінює лише один нейрон.

У другому – стан змінюється відразу у цілої групи нейронів, як правило, у всього шару. Далі розглядатимуться тільки синхронні НМ.

Мережі можна класифікувати також по числу шарів. Теоретично число шарів і число нейронів в кожному шарі може бути довільним, проте фактично воно обмежено ресурсами комп'ютера або спеціалізованою мікросхемою, на котрих звичайно реалізується ШНМ. Чим складніше ШНМ, тим масштабніші задачі, підвладні їй.

Вибір структури ШНМ здійснюється відповідно до особливостей і складності задачі. Для вирішення деяких окремих типів задач вже існують оптимальні, на сьогоднішній день, конфігурації. Якщо ж задача не може бути зведена ні до одного з відомих типів, розробнику доводиться вирішувати складну проблему синтезу нової конфігурації.

При цьому він керується декількома основоположними принципами:

- можливості мережі зростають із збільшенням числа шарів мережі і числа нейронів в них;

- введення зворотних зв'язків разом із збільшенням можливостей мережі піднімає питання про динамічну стійкість мережі;

- складність алгоритмів функціонування мережі (у тому числі, наприклад, введення декількох типів синапсів – збурюючих, гальмуючих і ін.) також сприяє посиленню потужності ШНМ.

Питання про необхідні і достатні властивості мережі для вирішення того або іншого роду задач являє собою цілий розділ нейрокомпьютерної науки. Оскільки проблема синтезу ШНМ сильно залежить від вирішуваної задачі, дати загальні докладні рекомендації тяжко.

У більшості випадків оптимальний варіант виходить на основі інтуїтивного вибору, хоча в літературі приведені докази того, що для будь-якого алгоритму існує нейронна мережа, яка може його реалізувати. Зупинимося на цьому докладніше.

Багато задач: розпізнавання образів (зорових, мовних і т.д.), виконання функціональних перетворень при обробці сигналів, управління, прогнозування, ідентифікації складних систем і т.д., зводяться до наступної математичної постановки.

Необхідно побудувати таке відображення X 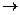Y , щоб на кожний можливий вхідний сигнал X формувався правильний вихідний сигнал Y. Відображення задається кінцевим набором пар ((вхід)®(відомий вихід)). Число таких пар (навчальних прикладів) істотно менше за загальне число можливих поєднань значень вхідних і вихідних сигналів.

Сукупність всіх навчальних прикладів носить назву навчальної вибірки.

У задачах розпізнавання образів X – деяке представлення образу (зображення, вектор чисел і т. д.), Y – номер класу, до якого належить вхідний образ.

У задачах управління X – набір контрольованих параметрів керованого об'єкту, Y – код, що визначає управляючу дію, відповідно поточним значенням контрольованих технологічних параметрів.

У задачах прогнозування в якості вхідних сигналів використовуються тимчасові ряди, що представляють значення контрольованих змінних на деякому інтервалі часу. Вихідний сигнал – множина змінних, які є підмножиною змінних вхідного сигналу.

При ідентифікації X і Y представляють вхідні і вихідні сигнали системи відповідно.

Взагалі кажучи, велика частина прикладних задач може бути зведена до реалізації деякого складного багатовимірного функціонального перетворення.

У результаті побудови такого відображення (тобто X 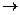Y) необхідно добитися того, щоб:

- забезпечувалося формування правильних вихідних сигналів відповідно до всіх прикладів навчальної вибірки;

- забезпечувалося формування правильних вихідних сигналів відповідно до всіх можливих вхідних сигналів, які не увійшли до навчальної вибірки.

Друга вимога в значній мірі ускладнює задачу формування навчальної вибірки. В загальному вигляді ця задача в даний час ще не вирішена, проте у всіх відомих випадках було знайдено окреме рішення. Подальші міркування припускають, що навчальна вибірка вже сформована.

Відзначимо, що теоретичною основою для побудови нейронних мереж є наступне:

Твердження. Для будь-якої кількості пар вхідних-вихідних векторів довільної розмірності {X_k , Y_k}, k=1...N існує двошарова однорідна нейронна мережа з послідовними зв’язками, з сигмоїдальними передаточними функціями і кінцевим числом нейронів, яка для кожного вхідного вектору X_k формує відповідний йому вихідний вектор Y_k.

Таким чином, для представлення багатовимірних функцій багатьох змінних може бути використана однорідна нейронна мережа, що має всього один прихований шар, з сигмоїдальними передаточними функціями нейронів.

Для оцінки числа нейронів в прихованих шарах однорідних нейронних мереж можна скористатися формулою для оцінки необхідного числа синаптичних ваг L_w (у багатошаровій мережі з сигмоїдальними передаточними функціями):

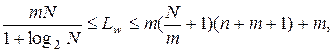(4.1)

де: n – розмірність вхідного сигналу, m – розмірність вихідного сигналу,

N – число елементів навчальної вибірки.

Оцінивши необхідну кількість ваг, можна розрахувати число нейронів у прихованих шарах. Наприклад, число нейронів у двошаровій мережі складе:

(4.2)

Відомі і інші подібні формули, наприклад, вигляду:

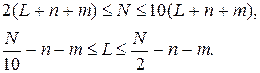(4.3)

Так само можна розрахувати число нейронів у мережах з великою кількістю шарів, які іноді доцільно використовувати: такі багатошарові нейронні мережі можуть мати менші розмірності матриць синаптичних ваг нейронів одного шару, ніж двошарові мережі, що реалізовують те ж саме відображення. На жаль, методики побудови таких мереж поки не існує.

Відзначимо, що вітчизняному фахівцеві приведені результати звичайно відомі у вигляді так званої теореми про повноту.

Теорема про повноту. Будь-яка безперервна функція на замкнутій обмеженій множині може бути рівномірно наближена функціями, обчислюваними нейронними мережами, якщо функція активації нейрона двічі безперервно диференційована.

Таким чином, нейронні мережі є універсальними апроксимуючими системами.

Очевидно, що процес функціонування ШНМ залежить від величин синаптичних зв'язків, тому, задавшись визначеною структурою ШНМ, розробник мережі повинен знайти оптимальні значення всіх змінних вагових коефіцієнтів (деякі синаптичні зв'язки можуть бути постійними).

Цей етап називається навчанням ШНМ, і від того наскільки якісно він буде виконаний, залежить здатність мережі вирішувати поставлені перед нею проблеми під час функціонування.

Контрольні питання

1. Основні топологічні типи нейромереж?

2. Типи багатошарових мереж?

3. Підхід до вибору структури нейромережі?

4. Дайте визначення навчальної вибірки?

5. Сформулюйте твердження про нейромережеве представлення багатовимірних функцій.

6. Сформулюйте теорему про повноту.