Алгоритм навчання Хебба

Сигнальний метод навчання Хебба полягає в зміні ваг за наступним правилом:

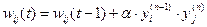(1)

де y_i^(n-1) – вихідне значення нейрона і шару (n-1), y_j⁽ⁿ⁾ – вихідне значення нейрона j шару n; w_ij(t) і w_ij(t-1) – вагові коефіцієнти синапсу, що з'єднує ці нейрони, на ітераціях t і t-1 відповідно; α – коефіцієнт швидкості навчання. Тут і далі, для спільності, під n мається на увазі довільний шар мережі. При навчанні по даному методу підсилюються зв'язки між збудженими нейронами. Існує також і диференційний метод навчання Хебба.

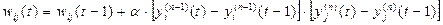(2)

Тут y_i^(n-1)(t) і y_i^(n-1)(t-1) – вихідне значення нейрона i шару n-1 відповідно на ітераціях t і t-1; y_j⁽ⁿ⁾(t) і y_j⁽ⁿ⁾(t-1) – те ж саме для нейрона j шару n. Як видно з формули (2), найсильніше навчаються синапси, які з'єднують ті нейрони, виходи яких найбільше динамічно змінилися убік збільшення.

Повний алгоритм навчання із застосуванням вищенаведених формул буде виглядати так:

1. На стадії ініціалізації всім ваговим коефіцієнтам присвоюються невеликі випадкові значення.

2. На входи мережі подається вхідний образ, і сигнали збудження поширюються по всіх шарах відповідно до принципів класичних прямопоточних (feedforward) мереж, тобто для кожного нейрона розраховується зважена сума його входів, до якої потім застосовується активаційна (передатна) функція нейрона, у результаті чого виходить його вихідне значення y_i⁽ⁿ⁾, i=0...M_i-1, де M_i – число нейронів у шарі i; n=0...N-1, а N – число шарів у мережі.

3. На підставі отриманих вихідних значень нейронів по формулі (1) або (2) виробляється зміна вагових коефіцієнтів.

4. Якщо вихідні значення мережі не застабілізуються із заданою точністю, перейти на крок 2.

На кроці 2 поперемінно пред'являються всі образи із вхідного набору.

Слід зазначити, що вид відгуків на кожен клас вхідних образів не відомий заздалегідь і буде являти собою довільне сполучення станів нейронів вихідного шару, обумовлене випадковим розподілом ваг на стадії ініціалізації. Разом з тим, мережа здатна узагальнювати схожі образи, відносячи їх до одного класу. Тестування навченої мережі дозволяє визначити топологію класів у вихідному шарі. Для приведення відгуків навченої мережі до зручного подання можна доповнити мережу одним шаром, що відображає вихідні реакції мережі в необхідні образи, наприклад, за алгоритмом навчання одношарового перцептрона.

Інший алгоритм навчання без учителя – алгоритм Кохонена – передбачає підстроювання синапсів на підставі їхніх значень від попередньої ітерації:

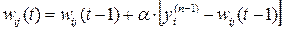(3)

З вищенаведеної формули видно, що навчання зводиться до мінімізації різниці між вхідними сигналами нейрона, що надходять із виходів нейронів попереднього шару y_i^(n-1), і ваговими коефіцієнтами його синапсів.

Повний алгоритм навчання має приблизно таку ж структуру, як у методах Хебба, але на кроці 3 із усього шару вибирається нейрон, значення синапсів якого максимально походять на вхідний образ, і підстроювання ваг по формулі (3) проводяться тільки для нього. Ця, так звана, акредитація може супроводжуватися загальмовуванням всіх інших нейронів шару і введенням обраного нейрона в насичення. Вибір такого нейрона може здійснюватися, наприклад, розрахунком скалярного добутку вектора вагових коефіцієнтів з вектором вхідних значень. Максимальний добуток дає нейрон, що виграв.

Інший варіант – розрахунок відстані між цими векторами в p-вимірному просторі, де p – розмір векторів:

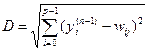, (4)

де j – індекс нейрона в шарі n, i – індекс підсумовування по нейронах шару (n-1), w_ij – вага синапсу, що з'єднує нейрони; виходи нейронів шару (n-1) є вхідними значеннями для шару n. Корінь у формулі (4) брати не обов'язково, тому що важлива лише відносна оцінка різних D_j.

У цьому випадку "перемагає" нейрон з найменшою відстанню. Іноді нейрони, які часто одержують акредитацію, примусово виключаються з розгляду, щоб "зрівняти права" всіх нейронів шару. Найпростіший варіант такого алгоритму полягає в гальмуванні нейрона, який щойно виграв.

При використанні навчання за алгоритмом Кохонена існує практика нормалізації вхідних образів, а так само – на стадії ініціалізації – і нормалізації початкових значень вагових коефіцієнтів:

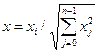, (5)

де x_i – i-а компонента вектора вхідного образу або вектора вагових коефіцієнтів, а n – його розмірність. Це дозволяє скоротити тривалість процесу навчання.

Ініціалізація вагових коефіцієнтів випадковими значеннями може привести до того, що різні класи, яким відповідають щільно розподілені вхідні образи, зіллються, або навпаки, роздрібняться на додаткові підкласи у випадку близьких образів того самого класу. Для запобігання такої ситуації використовується метод опуклої комбінації. Суть його зводиться до того, що вхідні нормалізовані образи піддаються перетворенню:

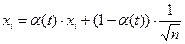, (6)

де x_i – i-а компонента вхідного образу, n – загальне число його компонентів, η(t) – коефіцієнт, що змінюється в процесі навчання від нуля до одиниці, у результаті чого спочатку на входи мережі подаються практично однакові образи, а із часом вони усе більше сходяться до вихідного. Вагові коефіцієнти встановлюються на кроці ініціалізації рівними величині

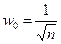, (7)

де n – розмірність вектора ваг для нейронів ініціалізованого шару.

На основі розглянутого вище методу будуються нейронні мережі особливого типу – так звані структури, що самоорганізуються, – self-organizing feature maps. Для них після вибору із шару n нейрона j з мінімальною відстанню D_j (4) навчається за формулою (3) не тільки цей нейрон, але і його сусіди, розташовані в околиці R. Величина R на перших ітераціях дуже велика, так що навчаються всі нейрони, але із часом вона зменшується до нуля. Таким чином, чим ближче кінець навчання, тим точніше визначається група нейронів, які відповідають кожному класу образів.