Основний принцип роботи мережі Кохонена
На рис. 1 наведений приклад топологічної карти мережі Кохонена, який складається із вхідного шару із n вхідних нейронів і шару Кохонена із m вихідних нейронів. Нейрони вхідного шару служать для введення значень ознак розпізнаваних образів. Активні нейрони шару Кохонена призначені для формування областей (кластерів) різних класів образів, при чому число цих кластерів апріорі невідоме. На рисунку показані зв'язки всіх вхідних нейронів лише з одним нейроном шару Кохонена. Кожен нейрон шару Кохонена також з'єднаний із сусідніми нейронами.
Пояснимо основний принцип роботи мережі Кохонена. Введемо наступні позначення (рис. 1):
wj=(wj1, wj2,…wj3)T,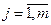 
(8)
– вектор вагових коефіцієнтів j-го нейрону шару Кохонена,
x=(x1, x2, …, xn)T (9)
– вхідний вектор або вектор значень ознак деякого зразка. На стадії навчання (точніше самонавчання) мережі вхідний вектор xc попарно порівнюється з усіма векторами wj всіх нейронів шару Кохонена. Вводиться деяка функція близькості (наприклад, у вигляді евклідової відстані). Активний нейрон з номером шару Кохонена, для якого значення функції близькості d(x,wc) між вхідним вектором х, що характеризує деякий образ, і вектором wc максимальне, оголошується "переможцем". При цьому образ, що характеризується вектором x, ставиться до класу, який є нейроном-"переможцем". В результаті здійснюється перетворення n-вимірного вхідного простору Rn на m-вимірну сітку (шар Кохонена).
Слід зауважити, що це відображення реалізується в результаті рекурентної (ітеративної) процедури самонавчання (Unsupervised Learning). Відмінна риса цього відображення – формування кластерів (Cluster) або класів. По завершенні процесу самонавчання на стадії реального використання мережі Кохонена невідомі вхідні образи відносяться до одного з виявлених кластерів (класів).
Виникає природне запитання: як виникає зазначене відображення топологічної карти? Для відповіді на нього розглянемо алгоритм самонавчання мережі Кохонена, вважаючи, що її вхідний шар містить n вхідних нейронів, а її шар Кохонена – m активних нейронів.
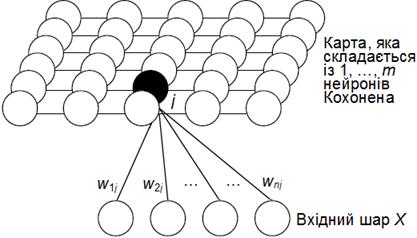
Рис. 1. Топологічна карта мережі Кохонена
Для визначення відстані між вхідним вектором x (9) і ваговим вектором wj (8) j-го нейрона шару Кохонена можна використати різні функції близькості (як правило, евклідову відстань).
При цьому "виграє" той нейрон c з ваговим вектором wc, що найбільш близький до вхідного вектора x:
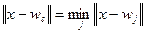(10)
або при використанні функції index, що визначає номер мінімальної відстані:
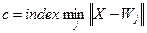(11)
При використанні скалярного добутку для нормованих векторів (векторів одиничної довжини)
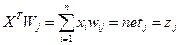(12)
"виграє" нейрон з максимальним значенням цього добутку.
На стадії самонавчання мережі Кохонена здійснюється корекція вагового вектора не тільки нейрона-"переможця", але й вагових векторів інших активних нейронів шару Кохонена, однак, звісно, в істотно меншій ступені – залежно від віддалення від нейрона-"переможця".
При цьому форма й величина околиці навколо нейрона-"переможця", вагові коефіцієнти нейронів якої також коректуються, у процесі навчання змінюються. Спочатку починають із дуже великої області – вона, зокрема, може включати всі нейрони шару Кохонена. Зміна вагових векторів здійснюється за правилом:
wj(t+1)=wj(t)+η(t)dcj(t)[x(t)–wj(t)], j=1…m (13)
де wj(t) – значення вагового вектора на t-му кроці самонавчання мережі, dcj(t) – функція близькості між нейронами шару Кохонена (neighborhood Kernel) і η(t) – змінюваний у часі коефіцієнт корекції. У якості η(t), як правило, вибирається монотонно зменшувана функція 0<η(t)<1, тобто алгоритм самонавчання починається порівняно великими кроками адаптації і закінчується відносно невеликими змінами.
Зверніть увагу, що згідно з (13) зміна того або іншого вагового вектора wj пропорційна відстані між вхідним вектором x і цим ваговим вектором.
Як приклад розглянемо мережу Кохонена з одновимірним шаром Кохонена (рис. 2). На рисунку наведений рух вагових векторів нейронів шару Кохонена. До вхідного вектора x ближче всіх розташований ваговий вектор w5 для нейрона c=5. Цей ваговий вектор змінюється найбільше: він більшою мірою наближається до вхідного вектора x. На другому місці за ступенем близькості перебувають вагові вектори w4 і w6. Зміна їх – друга по силі (ступеню). Вагові вектори w3 і w7 також змінюються, однак в істотно меншому ступені.
Нейрони 1, 2, 8 і 9 розташовані поза околицею навколо нейрона-"переможця" c=5, тому їхні вагові вектори залишаються без зміни після показу мережі образу, що характеризується вектором x.
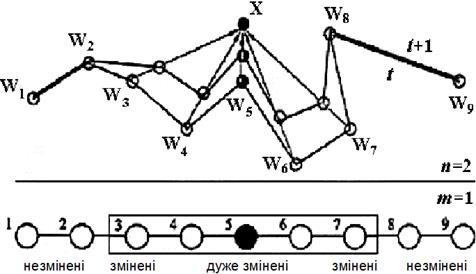
Рис. 2. Мережа Кохонена з одновимірним шаром Кохонена
Приведемо приклади функцій близькості (двовимірного шару Кохонена). Відстань між нейронами i й j у двовимірному просторі:
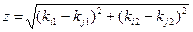, (14)
де ki1 і ki2 – координати по осі x і осі y нейрона i; kj1 й kj2 – аналогічно для нейрона j. При цьому можна використати наступні функції близькості:
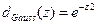; (15)
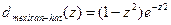; (16)
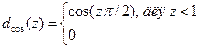. (17)
Як зазначено вище, зміна вагових векторів wj здійснюється в напрямку вхідного вектора x багаторазово. У процесі самонавчання варіюється як коефіцієнт корекції η, так і радіус d, який задає околицю навколо нейрона-"переможця".
Дата добавления: 2015-10-09; просмотров: 1373;