Збіжність алгоритму самонавчання

При розгляді проблеми збіжності обмежимося найпростішим одномірним випадком, коли є лише один вхід. Нехай [a, b] – область значень для входу (замкнутий інтервал). Покажемо, що алгоритм самонавчання переводить вагу x у середину інтервалу (рис. 3).

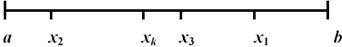
Рис. 3. Область значень для введення

Нехай x₁ – початкове значення ваги одного активного нейрона шару Кохонена. Це значення x₁ вибирається випадково: інтервал [a, b] розбивається на 2 підінтервали [a, x₁] і [x₁, b]. Кожна зміна x визначається його відстанню до a і до b: dx/dt=η(b–x)/2+η(a–x)/2=η((a+b)/2–x).

Для зміни ваги x у точці x₁ слід

Δx₁=η((a+b)/2–x₁). (18)

Позначимо y_i=x_i–(a+b)/2, тоді співвідношення (18) можна подати так: Δx₁=–ηy₁. Визначимо математичне очікування для значення ваги x₂ на наступному кроці алгоритму самонавчання:

x₂=x₁+Δx₁=(a+b)/2+y₁–ηy₁=(a+b)/2+y₁(1–η).

Аналогічно можна визначити і x₃: x₃=(a+b)/2+y₁(1–η)² або в загальному випадку: x_k=(a+b)/2+y₁(1–η)^k-1. При ηÎ[0,1] значення x_k сходиться до (a+b)/2.

Розширимо розглянутий одномірний випадок і припустимо, що одномірний шар Кохонена (лінійка) містить не один нейрон (як раніше), а m активних нейронів з вагами x₁, x₂, …, x_m... Припустимо, що ці ваги упорядковані 0<x₁<x₂<…<x_m<b і рівномірно розподілені в інтервалі [a, b]. У цьому випадку в процесі самонавчання вагові коефіцієнти сходяться до значень (рис. 4):

x_i=a+(2i–1)(b–q)/2m, i=1, 2, …, m,... (19)

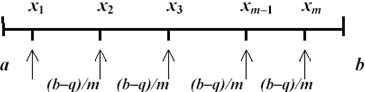
Рис. 4. Розподіл вагових коефіцієнтів

Звернемо увагу, що точки (19) для ваг x_i, i=1, 2, …, m визначають найбільш стійкі позиції, тому що dx_i/dt=0. У двовимірному випадку шар Кохонена містить m×m активних нейронів, а областю визначення для входів є декартовий добуток [a, b]×[c, d], тобто вхідний шар містить 2 нейрони. У цьому випадку ваговий вектор кожного нейрона шару Кохонена має дві складові – за числом входів. Кожен нейрон шару Кохонена також характеризується двома координатами – за віссю абсцис і за віссю ординат.

Подібно одномірному випадку можна показати, що координати вагових векторів нейронів шару Кохонена на осі абсцис у процесі самонавчання рівномірно розподіляються в інтервалі [a, b]: 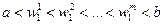. Аналогічно для координат цих векторів по осі ординат: .

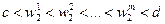У результаті самонавчання мережі Кохонена вагові вектори нейронів шару Кохонена рівномірно розподіляються у вхідному просторі.