Побудова евристичного алгоритму розпізнавання
Аналіз некоректних алгоритмів дозволив виявити принципи їх формування, а їх формалізація дозволила отримати математичні моделі евристичних алгоритмів розпізнавання.
Розглянемо процес побудови такої моделі на прикладі формалізації принципу розділення. Суть його в тому, що там, де описи об’єктів задаються наборами значень числових ознак (об’єкти є точками n-мірного простору), такі описи, що належать різним класам, можуть бути розділені поверхнями достатньо простого виду.
Розглянемо одну з можливих формалізацій. Скористаємося найпростішим класом розділюючих поверхонь – гіперпрлощинами
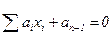 (1)
(1)
Нехай множина допустимих об’єктів розділена на два класи 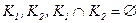 .
.
Відомо, що об’єкти S1, …, Sm належать К1 , а об’єкти Sm+1, …, Sq до К2. Ці об’єкти не рівнозначні, тому введемо їх числові характеристики γ(Si)=гi – вага об’єкта Si, і=1, 2, …, m, m+1, q. Отже множина алгоритмів характеризується заданням параметрів а1, …, аn+1 – коефіцієнтів у рівнянні гіперплощини і г1, …, гq – вагою об’єктів, класифікація яких проведена раніше.
Процес розпізнавання для I(S)=(б1, …, бn) відбувається наступним чином.
Нехай
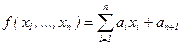 .
.
Розділимо об’єкти S1, …, Sm на множини 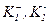 :
: 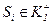 якщо
якщо 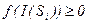 ;
; 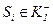 якщо
якщо 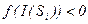 .
.
Аналогічно розділимо об’єкти Sm+1, …, Sq на множини 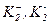 . Розглянемо величини
. Розглянемо величини
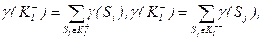
і аналогічно їм величини
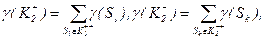
тут 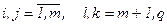 .
.
Обчислюємо 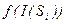 . Поставимо у відповідність S два число:
. Поставимо у відповідність S два число: 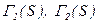 – що відповідно значеннями функції незалежності S класам К1, К2.
– що відповідно значеннями функції незалежності S класам К1, К2.
Якщо 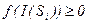 , то
, то
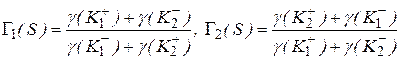 (2)
(2)
Якщо 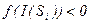 , то
, то
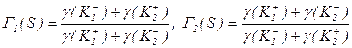 (3)
(3)
По значенням 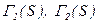 приймається рішення про віднесення S в клас К1 або К2. Ця процедура задається рішаючим правилом.
приймається рішення про віднесення S в клас К1 або К2. Ця процедура задається рішаючим правилом.
Розглянемо клас рішаючих правил, які визначаються параметром d.
Якщо 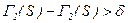 , тоді
, тоді 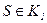
Якщо 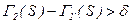 , тоді
, тоді 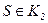
Якщо 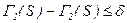 , тоді рішення не приймається, алгоритм відмовляється від класифікації S.
, тоді рішення не приймається, алгоритм відмовляється від класифікації S.
Це є реалізація однієї з можливих моделей, основаних на принципі розділення.
Основні гіпотези, які використано:
1) елементи класів К1, К2 розділяються гіперплощиною;
2) елементи класів не рівнозначні по важливості; міру цієї важливості можна виразити числом.
Реалізація гіпотез проведена при побудові моделей
М(а1, … аn+1, g1, …, gq, d),
-¥<gi, ai<+¥,
d³0.
Задання значень всіх параметрів моделі визначає її елемент – конкретний алгоритм розпізнання.
Дата добавления: 2015-09-11; просмотров: 728;
