Відношення порядку на множині невід’ємних раціональних чисел.
4. Розглянемо правила порівняння невід’ємних раціональних чисел, причому намагатимемося ввести їх таким чином, щоб вони не суперечили правилам порівняння цілих чисел. Розглянемо спочатку два невід’ємних раціональних числа а= 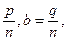 з однаковими знаменниками. Будемо вважати, що
з однаковими знаменниками. Будемо вважати, що 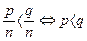 . Як же бути у випадку дробів з різними знаменниками? Для відповіді на поставлене запитання приймемо наступні означення.
. Як же бути у випадку дробів з різними знаменниками? Для відповіді на поставлене запитання приймемо наступні означення.
Означення: з двох невід’ємних раціональних чисел з однаковими знаменника меншим (більшим) буде те, у якого чисельник менший (більший).
Означення: з двох дробів з різними знаменниками 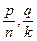 меншим (більшим) буде той, для якого справджується нерівність pk<qn (pk>qn).
меншим (більшим) буде той, для якого справджується нерівність pk<qn (pk>qn).
Перше означення символічно можна записати так: ( 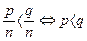 ), а друге – (
), а друге – ( 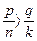 )Û(pk>qn).
)Û(pk>qn).
З’ясуємо, які властивості має це відношення. Оскільки нерівності а<а і а>а не можуть бути одночасно істинними, то це відношення має властивість антирефлексивності. Для виявлення інших властивостей доведемо наступні теореми.
Теорема: для будь-яких невід’ємних раціональних чисел  і
і 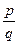 , якщо
, якщо  <
< 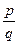 , то
, то 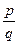 >
>  .
.
Символічно сформульована теорема запишеться так: ("  єQ0)("
єQ0)(" 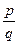 єQ0)[(
єQ0)[(  <
< 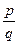 )Þ(
)Þ( 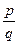 >
>  )].
)].
Доведення.
За означенням, якщо  <
< 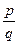 , то mq<pn. Тоді pn>mq, тобто
, то mq<pn. Тоді pn>mq, тобто 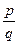 >
>  . Що й треба було довести.
. Що й треба було довести.
Теорема: для будь-яких невід’ємних раціональних чисел а, b, с, якщо (а<bÙb<c),то a<c.
Символічно ця теорема запишеться так: ("а,b,сєQ0)[(а<bÙb<c)→(a<c)].
Доведення.
 Розглянемо невід’ємні раціональні числа такі, що
Розглянемо невід’ємні раціональні числа такі, що 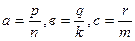 . Тоді маємо:
. Тоді маємо: 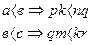 →pk<nq<qm<kr→pm<nr→
→pk<nq<qm<kr→pm<nr→ 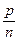 <
< 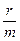 →a<c. Що й треба було довести.
→a<c. Що й треба було довести.
Доведені теореми виражають відповідно властивості асиметричності та транзитивності. Таким чином, можна стверджувати, що відношення «менше» («більше») на множині невід’ємних раціональних чисел має властивості антирефлексивності, асиметричності та транзитивності, а тому воно є відношенням строгого порядку.
Дата добавления: 2015-11-04; просмотров: 1091;
