Введение в метод конечных разностей
Функции, которые находят в результате решения ДУЧП Лапласа и Пуассона, имеют непрерывный характер. Поиск решения начинается с представления искомой функции в виде таблицы, которая задает значения функции в некоторых точках области ее определения. Предполагается, что между указанными точками области искомая функция изменяется по известному, например линейному, закону. При построении дискретной модели непрерывной величины 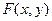 поступают следующим образом:
поступают следующим образом:
- область определения искомой функции 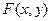 делят на конечное число подобластей, называемых дискретами;
делят на конечное число подобластей, называемых дискретами;
- в центре каждой дискреты фиксируются точки – узлы;
- значение 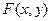 в каждом узле считается неизвестной переменной, подлежащей определению;
в каждом узле считается неизвестной переменной, подлежащей определению;
- в дискретах определяется среднее значение производных 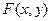 первого и второго порядка.
первого и второго порядка.
Продемонстрируем метод конечно-разностной аппроксимации на примере определения двумерной функции 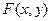 в заданной области
в заданной области 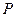 . Разобьем область
. Разобьем область 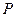 на дискреты ортогональной сеткой с шагом
на дискреты ортогональной сеткой с шагом 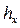 и
и 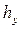 по осям
по осям 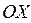 и
и 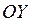 соответственно. Пусть
соответственно. Пусть 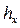 =
= 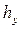 =
= 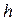 . Пронумеруем дискреты по осям, начиная от начала координат. Обозначим через
. Пронумеруем дискреты по осям, начиная от начала координат. Обозначим через 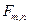 - значение функции в центре дискреты с номерами
- значение функции в центре дискреты с номерами 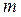 и
и 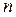 соответственно по осям OX и OY (рисунок 3).Осуществим предельный переход для разностей типа:
соответственно по осям OX и OY (рисунок 3).Осуществим предельный переход для разностей типа: 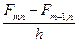 и
и 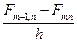 при измельчении шага сетки
при измельчении шага сетки 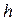 . В пределе это отношение стремится к постоянной величине, определяемой тангенсом угла наклона касательной к кривой сечения поверхности, задаваемой функцией F, в точке
. В пределе это отношение стремится к постоянной величине, определяемой тангенсом угла наклона касательной к кривой сечения поверхности, задаваемой функцией F, в точке 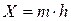 , то есть – к производной F в этой точке:
, то есть – к производной F в этой точке:
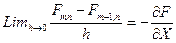 ;
; 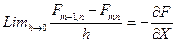
Следовательно, обе разности заменяются одной и той же производной. При обратном переходе от производной к разностям производные заменяются так:
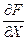 ®
® 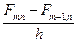 ;
; 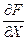 ®
® 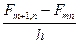
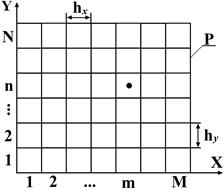
Рис.3. Дискретное рабочее поле
В первом случае разность называется левой, а во втором – правой. Аналогичный переход выполним для производных по оси OY:
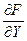 ®
® 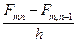 ;
; 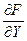 ®
® 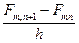
Рассмотрим следующие отношения:
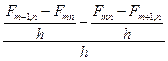 и
и 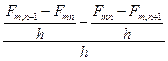
При стремлении h® 0 эти отношения стремятся соответственно к значениям: 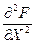 и
и 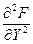 в точке
в точке 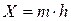 и
и 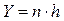 . Следовательно, при обратном переходе от вторых производных к разностям можно заменять производные так:
. Следовательно, при обратном переходе от вторых производных к разностям можно заменять производные так:
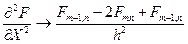 и
и 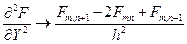
С помощью этих переходов можно производить замену производных в дифференциальных уравнениях, которые превращаются в разностные, а сами разности, заменяющие производные называют конечными разностями.
Метод решения задачи, записанной в виде ДУ, с помощью разностного уравнения называют методом конечных разностей, при котором решение собственно ДУ заменяется решением системы линейных алгебраических уравнений с количеством неизвестных, равных количеству дискрет разбиения области определения функции F.
Рассмотрим уравнение Пуассона вида: 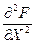 +
+ 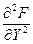 = f(x,y).
= f(x,y).
Переходя от вторых производных к конечным разностям в точке (mh, nh) области Р, получим разностное уравнение вида:
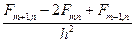 +
+ 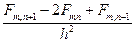 = f(x,y).
= f(x,y).
Формируя это уравнение для всех точек области Р, получим систему алгебраических уравнений с числом неизвестных равным числу дискрет области:
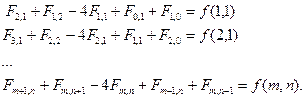 (4)
(4)
При заданных на границе области Р значениях функции f данное уравнение может иметь единственное решение, которое и определит дискретную модель непрерывной величины F в области Р.
«АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА В ПАССИВНОЙ ЭЛЕКТРИЧЕСКОЙ СХЕМЕ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ»
Дата добавления: 2015-09-07; просмотров: 1562;
