МЭМС-акселерометр маятникового типа

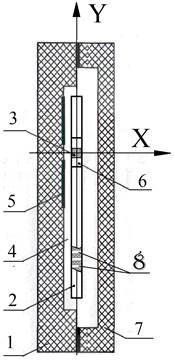
Микромеханический акселерометр представляет собой капсулированный элемент, образованный корпусом 1, выполненным в виде платы из диэлектрического материала с напыленными на ней неподвижными электродами 5 емкостного датчика угла и электростатического датчика момента и диэлектрической крышки 7, скрепленной с корпусом 1. Основа акселерометра – монокристаллический кремниевый маятник 0,8´1,0´0,015 мм (инерционная масса2) подвешена с зазором на плате в виде маятника на упругих перемычках – торсионах 3 за опорный элемент 6. Торсионы представляют собой устройство демпфирования сечением 0,012 ´0,015 мм, которое позволяет инерционной массе останавливаться при полном диапазоне колебаний, защищая устройство от механического удара. Инерционная масса, торсионы и опорный элемент выполнены в форме прямоугольника, на поверхности которого равномерно распределены сквозные отверстия (2).

Внутрь корпуса закачивается газовая смесь, которая обеспечивает демпфирование собственных колебаний инерционной массы 2. Крышка также выполняет функцию ограничителя перемещений инерционной массы 2 при вибрационных и ударных воздействиях.

Напылённые электроды емкостного датчика угла и электростатического датчика моменты выполнены единым элементом и в совокупности представляют собой электронную схему обработки сигналов.

Для данного варианта конструкции ось чувствительности (OX) ортогональна плоскости чувствительного элемента. Маятник изготовлен вместе с упругими торсионами по технологии "кремний на стекле".

Принцип функционирования - при действии ускорения в направлении оси чувствительности Х-Х инерционная масса 2 отклоняется от своего исходного состояния. При этом изменяются величины емкостей конденсатора, образованного неподвижными электродами 5 и инерционной массой 2. Съем информации производится с помощью емкостного датчика перемещений. Сигнал отклонения преобразуется электронной схемой и приводит к возникновению электростатического момента, стремящегося возвратить инерционную массу 2 в исходное состояние. В установившемся состоянии сигнал с выхода электронной схемы является выходным сигналом микромеханического акселерометра.

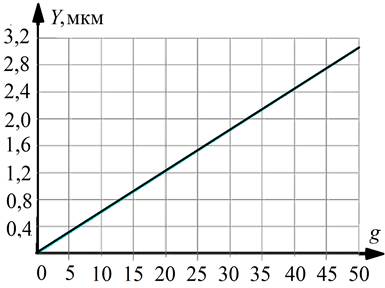
График зависимости перемещения чувствительного элемента маятникового типа от преобразуемого им линейного ускорения приведен на рисунке 6.5 [3].

Рис. 6.5. График зависимости перемещения инерционной массы акселерометра маятникового типа от воздействия линейного ускорения

Методология проектирования МЭМС базируется на классической электродинамике Максвелла, классической механике Ньютона и теоретической механике Лагранжа. Математическими моделями на междисциплинарном уровне являются дифференциальные уравнения в частных производных (ДУЧП). Примерами моделей могут служить уравнения математической физики с заданными краевыми условиями, характеризующими пространственное распределение переменных в на­чальный момент времени, и граничные условия, задающие значения этих переменных на границах рассматриваемой области.

В большинстве САПР, используемых при проектировании МЭМС, используются:

- метод конечных разностей (МКР);

- метод конечных элементов (МКЭ);

- метод граничных элементов (МГЭ).

МКР работает непосредственно с исходным ДУЧП и/или ОДУ, переводя его в общем случае в систему конечно-разностных уравнений, приближенно описывающую поведение искомой функции в i-ом узле сетки.

Метод конечных элементов (МКЭ) практически не имеет конкурентов в области численного решения задач инженерного анализа МЭМС.

У метода конечных элементов есть твердая теоретическая основа. Она базируется на математических теоремах, которые гарантируют асимптотическое приближение результата расчета поля к точному решению при уменьшении размеров конечных элементов, используемых в процессе решения. Он не работает непосредственно с исходным ДУ, а использует вариационную его трактовку в виде функционала, минимизация которого позволяет форсированно получить матрицы (так называемые «матрицы жесткости») конечных элементов, которые собственно и используются в САПР как модели конечных элементов.

САПР выполняет моделирование МЭМС в конечной области пространства с соответствующими граничными и/или начальными условиями. Геометрия задачи при этом автоматически разбивается генератором сетки на конечные элементы, которые покрывают всю область решения.

Когда сетка построена, в определенных точках объекта задаются начальные условия (точки закрепления, нагрузки и пр.), представляющие внешние и/или внутренние воздействия фазовых переменных на объект. Далее, выполняется собственно моделирование. Как правило, анализ влияния нескольких фазовых переменных на изменение состояния МЭМС и НЭМС выполняется по отдельности, поскольку затруднительно промоделировать их в связанной постановке. Основная сложность одновременного моделирования воздействия нескольких фаз на объект заключается в необходимости получения совместного согласованного решения уравнений, которыми описываются влияние каждой фазовой переменной на объект. Такие задачи называются «связанными»