ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. 1. Запишем уравнение Кирхгофа для заданной схемы (рис.9).
1. Запишем уравнение Кирхгофа для заданной схемы (рис.9).
2. Шаг дискретизации по времени примем равным D=RC/10.
3. Переходим к конечно-разностному представлению системы:
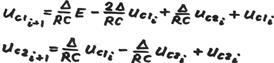
4. Программа расчета переходного процесса приведена на рис.10:
| const R=1e+3; C=1e-6; E=1.0; n=200; var a,b,d,t:real;m1,m2:array[1..n]of real; i:integer; begin for i:=1 to n do m1[i]:=0; for i:=1 to n do m2[i]:=0; t:=(R*C)/10; d:=1/(R*C); a:=d*E; b:= 2/(C*R); i:=1; repeat m1[i+1]:=t*a-t*b*m1[i]+t*d*m2[i]+m1[i]; m2[i+1]:=t*d*m1[i]-t*(1/(R*C))*m2[i]+m2[i]; i:=i+1; until m1[i]-m1[i-1]<0.01; end. | Const n=250; E=1; c=1e-6;L=20e-3; r=1000.0; Var MuC: array[1..n]of real; i,j,k:integer; BEGIN For i:=1 to n do MuC[i]:= 0; i:=2; repeat MuC[i+1]:=MuC[i]+((E-MuC[i-1])/(1+R*sqrt(C/L))); for k:=0 to 5 do begin for j:=1 to 10 do write(MuC[k*10+j]:5:3,' '); writeln; end; i:=i+1; writeln; until MuC[i]-MuC[i-1]<0.0001; readln; END. |
| Рис.10 | Рис.11 |
Дата добавления: 2015-09-07; просмотров: 1030;
