I. Теоретическое введение
Известно, что разнообразные действия света обусловлены в первую очередь наличием определенной световой энергии. Непосредственное восприятие света обусловлено действием световой энергии, поглощенной чувствительными элементами глаза. То же имеет место и в любом приемнике, способном реагировать на свет, например, в фотоэлементе, термоэлементе и фотопластинке.
Количество световой энергии W ,проходящей через какую-либо площадку в единицу времени, называется потоком лучистой энергии через эту площадку.
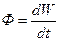 (1)
(1)
Поток лучистей энергии, оцениваемый по зрительному ощущению, называется световым потоком.
Все вопросы, связанные с определением световых величин, особенно просто решаются в том случае, когда источники света являются точечными. Назовем точечным такой источник света, размеры которого малы по сравнению с расстоянием до места наблюдения и который (в однородной и изотропной среде) излучает сферические волны. Для характеристики точечных источников света применяется сила света I, которая определяется как световой поток приходящий на единицу телесного угла;
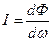 (2)
(2)
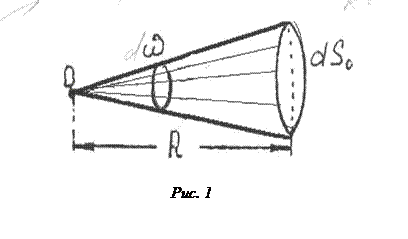
Телесный угол ω равен отношению поверхности dS, вырезанной на сфере конусом с вершиной "О" (рис. 1), к квадрату радиуса сферы: 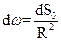
В случае сферы 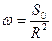 .
.
Единицей телесного угла является стерадиан - телесный угол, которому на сфере единичного радиуса соответствует поверхность с площадью, равной единице. Полный телесный угол равен 4π.
 |
Сила света, измеряется в международных свечах (канделах). Кандела является одной из основных единиц Международной системы (СИ).
Единицей светового потока является люмен (лм). Он равен световому потоку, излучаемому изотропным источником с силой света в 1 кд. в пределах телесного угла в один стерадиан, из формулы (2) следует:
dФ=I dω => 1лм = 1кд · 1стер.
Освещенность Е поверхности S определяется световым потоком, падающим на единицу площади этой поверхности.
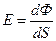 (3)
(3)
Единицей - освещенности является люкс (лк), равный освещенности, создаваемой потоком в 1 лм, равномерно распределенным по поверхности в 1м2:
1лк=1лм/1м2 (см. формулу (3))
Как показывают формулы (2) и (3) величины Е и I связаны между собой.
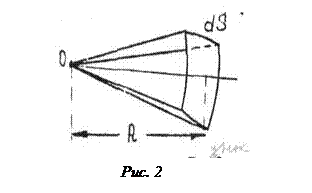 |
Пусть точечный источник О освещает небольшую площадку dS, расположенную на расстоянии R от источника (рис.2).
Построим телесный угол, вершина которого лежит в т. О и который опирается на края площадки dS. Величина этого угла dω=dS/R2.
Поток, посылаемый нашим источником через этот телесный угол, обозначим через dФ. Тогда сила света
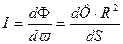 (4)
(4)
Освещенность
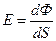 (5)
(5)
Из формулы (4) следует, что
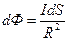 .
.
Подставим это значение dФ в формулу (5), тогда
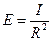 , (6)
, (6)
то есть освещенность площадки при перпендикулярном падении лучей равна силе света, деленной на квадрат расстояния до точечного источника.
Сравнивая освещенности площадок, расположенных на разных расстояниях от точечного источника, найдем
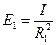 ;
; 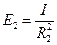 — или, разделив первое на второе,
— или, разделив первое на второе,
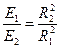 (7)
(7)
то есть освещенность обратно пропорциональна квадрату расстояния от площадки до точечного источника. Это так называемый закон обратных квадратов или первый закон освещенности.
Если бы площадка dS была расположена не перпендикулярно к оси потока, а повернута на угол α (рис.3), то она имела бы размеры
dS=dSo /cosα , (8)
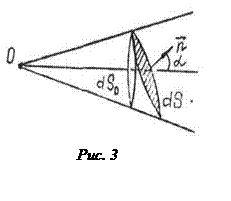 |
где dSo-площадка, пересекающая тот же телесный угол перпендикулярно к оси пучка, так что
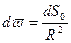 (9)
(9)
Мы предполагаем площадки dS и dSo настолько малыми и столь удаленными от источника, что для всех точек этих площадок расстояние до источника может считаться одинаковым (R) и лучи во всех точках составляют с перпендикуляром к площадке dS один и тот же угол α (угол падения).
В таком случае освещенность площадки dS есть
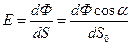
или 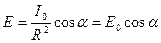 , (10)
, (10)
где 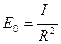 - освещенность при нормальном падении света на площадку.
- освещенность при нормальном падении света на площадку.
Итак, освещенность, создаваемая точечным источником на некоторой площадке, равна силе света, умноженной на косинус угла падения света на площадку и деленной на квадрат расстояния от источника до данной площадки. Это II закон освещенности.
Дата добавления: 2015-10-13; просмотров: 2226;
