I. Теоретическое введение. Магнитная индукция – векторная величина, модуль которой равен максимальному значению силы Ампе­ра, действующей на прямой провод­ник с током длиной 1 м

Магнитная индукция – векторная величина, модуль которой равен максимальному значению силы Ампе­ра, действующей на прямой провод­ник с током длиной 1 м, по которому течет ток 1 А.

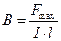(1)

За единицу магнитной индукции приня­та тесла (сокращенно: Тл),

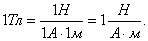
Если в некоторой области пространст­ва вектор индукции магнитного поля имеет одинаковое значение по мо­дулю и одинаковое направление во всех точках поля, то магнитное поле в этом пространстве называется однородным.

Кроме магнитной индукции магнитное поле описывается величиной, называемой напряженностью магнитного поля. Она связана с вектором магнитной индукции формулой:

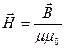, (2)

где μ = 1 + χ (3)

µ₀ = 4π·10^-7 Гн/м – магнитная постоянная.

аχ – магнитная восприимчивость.

Для ферромагнетиков μ >> 1 , χ >> 0.

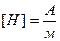- единица измерения напряженности магнитного поля.

Элементарным магнитным потоком dФ через малую пло­щадку dS называется величина, равная произведению мо­дуля вектора индукции на площадь и косинус угла между вектором ин­дукции и нормалью к площадке:

dФ = ВdSсоsα. (4)

В однородном магнитном поле маг­нитный поток через плоскую площад­ку равен:

Ф = ВSсоs α. (5)

В произвольном магнитном поле полный поток определяется по формуле:

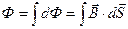(6)

За единицу магнитного потока в СИ принят вебер (сокращен­но: Вб).

1 Вб = 1 Тл·1 м² .

В магнитных полях линии индук­ции всегда замкнуты и образуют вихревое поле. В результате замкнутая поверхность, помещенная в магнитное поле, пронизывается ли­ниями магнитной индукции так, что любая линия, входящая в эту по­верхность, выходит из нее. Следова­тельно, полный магнитный поток че­рез произвольную замкнутую поверх­ность равен нулю.

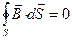. (7)

Данное утверждение носит название теоремы Гаусса.

Полученный ре­зультат является следствием того факта, что в природе нет магнит­ных зарядов, и магнитные поля об­разуются только электрическими токами.