I. Теоретическое введение. Дифракцией света называется явление отклонения световой волны от направления своего первоначального прямолинейного распространения
Дифракцией света называется явление отклонения световой волны от направления своего первоначального прямолинейного распространения, если на её пути встречается какое-либо непрозрачное тело, размеры которого соизмеримы с длиной волны.
Наблюдение дифракции основано на том, что отклонённые световые волны, интерферируя друг с другом, образуют своеобразное распределение энергии в виде закономерно чередующихся максимумов и минимумов.
Для получения дифракционной картины применяется дифракционная решётка, представляющая собой стеклянную пластинку, на поверхности которой на расстоянии 0,01 – 0,001 мм наносятся царапины, которые затем заливаются тушью. Такие царапины – штрихи представляют собой непрозрачные, закономерно расположенные препятствия (в), разделённые прозрачными промежутками (а). Если на решётку падает плоская волна, фронт которой параллелен плоскости решётки, то тогда по принципу Гюйгенса каждая точка волнового фронта в любой момент является источником вторичных волн.
Направления, в которых распространяется энергия этих волн, называются лучами. Плоской волне соответствует нормально расположенные к её поверхности параллельные лучи. Явление дифракции в параллельных лучах называется дифракцией Фраунгофера.
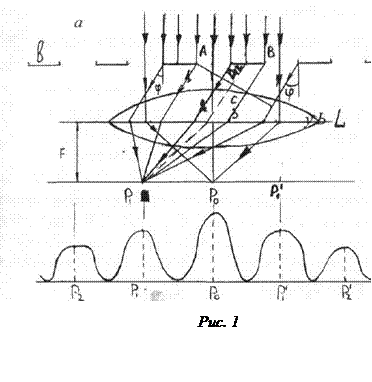 |
Если на дифракционную решётку падает поток параллельных лучей (рис. 1), то падая в области (а), он проходит через них, не изменяя своего первоначального направления. Лучи, попадающие в области (в), совсем не проходят через них, поглощаясь слоем туши. На границах же областей (в) и (а), согласно принципу Гюйгенса, образуется целый веер отклонённых в разных направлениях лучей (рис.1).
Если на пути, прошедших через решётку лучей, поставить собирающую линзу (L), то в различных точках её фокальной плоскости происходит интерференция взаимно параллельных лучей.
Усиление света происходит в точках Р1, Р1¢, Р2, Р2¢ (рис.1), в которых встречаются световые лучи с разностью хода D = ± kl и разностью фаз
Dy = 2kp (k = 1, 2, 3…).
Ослабление света имеет место при наложении световых лучей с разностью хода D = (2k + 1) 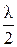 и разностью фаз Dy = (2k + 1)p.
и разностью фаз Dy = (2k + 1)p.
Интерференционная картина, образующаяся в фокальной плоскости линзы, носит название дифракционного спектра.
Угол между первоначальным направлением светового луча и его направлением после дифракции называется углом дифракционного отклонения (угол j на рис.1).
Рассмотрим случай одной щели. Для этого разобьём участок плоского волнового фронта, соответствующий одному прозрачному промежутку "а" (ширина щели) на зоны Френеля.
Зонами Френеля называются такие воображаемые участки на поверхности волнового фронта, от которых световые лучи идут до точки наблюдения Р с разностью хода изменяющейся на λ/2 с изменением номера зон.
От двух соседних зон вторичные волновые процессы приходят в точку Р в противофазе и при наложении ослабляют друг друга (рис.2).
 |
Расстояния от каждой зоны Френеля до точки наблюдения Р при этом определятся следующим образом:
r1 = r0 + 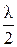
r2 = r1 + 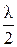 = r0 + 2
= r0 + 2 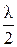
r3 = r2 + 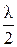 = r0 + 3
= r0 + 3 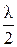 и т.д.
и т.д.
………………………….
rn = rn-1 + 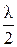 = r0 + n
= r0 + n 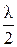
Результирующая амплитуда в точке наблюдения Р определяется формулой:
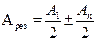
где А1 – амплитуда колебаний, приходящих в точку Р от первой зоны (область между r1 и r1¢) (рис.2);
Аn – амплитуда от последней зоны;
n – число зон, укладывающихся на длине а, равной ширине щели.
От двух соседних зон (например 1-ой и 2-ой) волновые процессы проходят в противоположных фазах, т.к. они проходят пути, отличающиеся друг от друга на 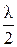 , следовательно, при n = 2
, следовательно, при n = 2
Арез = 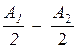 .
.
Подобное равенство будет иметь место при любом четном числе зон Френеля, например, при n = 2k, где k = 1, 2, 3, 4… Условие минимума в этом случае имеет вид:
Арез = 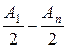 .
.
При нечётном числе зон Френеля (n = 2k + 1) амплитуды от 1-ой и n-ой зон будут в одной фазе и, следовательно, будут складываться друг с другом:
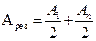 .
.
Это будет соответствовать условию максимума.
Число зон Френеля на ширине промежутка (а) зависит от угла дифракционного отклонения j световых лучей 1 и 2 (рис.1). Их геометрическая разность хода D1 – 2 определяется формулой:
D1 – 2 = а × sin j. (2)
Если на отрезке "а" укладывается n зон Френеля, то 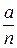 представляет собой протяжённость одной (например i-ой) зоны. Тогда между лучами 1¢ и 2¢, распространяющимися под углом j от начала и конца i-ой зоны существует разность хода
представляет собой протяжённость одной (например i-ой) зоны. Тогда между лучами 1¢ и 2¢, распространяющимися под углом j от начала и конца i-ой зоны существует разность хода 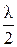 (рис.3).
(рис.3).
 |
Из треугольника для i-ой зоны имеем: sin j =
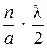 .
.
Подставляя это значение в формулу (2) для D1-2 получим:
D1-2 = 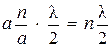 .
.
То есть для лучей 1 и 2, отклонённых противоположными краями одной и той же щели в определённом направлении j, разность хода зависит от числа зон Френеля. Получим ли мы в этом направлении максимум или минимум зависит от того, будут ли n чётными или нечётными.
Таким образом, для дифракции от щели имеем следующие условия:
а) для максимума n должно равняться (2k + 1), где k = 1, 2, 3, …. В этом случае должна существовать разность хода между лучами 1 и 2:
D1-2 = а × sin j = (2k + 1) 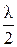 ;
;
б) для минимума n должно быть равно 2k и разность хода будет:
D1-2 = а × sin j = (2k 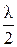 ) = kl.
) = kl.
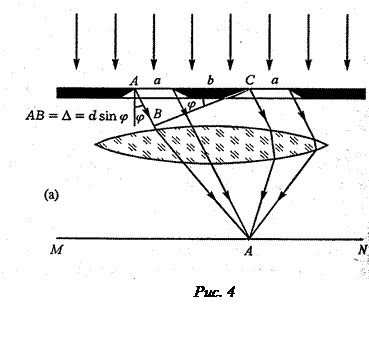
Рассмотрим теперь случай двух и более щелей (рис.4).
Предположим, что лучи 1 и 3 распространяются в направлении, при котором в каждой щели а1 и а2 укладывается нечётное число зон Френеля, а, следовательно, имеет место максимум интерференции для каждой из щелей в
 |
отдельности.
Лучи взаимно усиливаются, если они придут в точку в одинаковой фазе, ослабляются, если их фазы в этой точке будут противоположными.
Разность фаз лучей зависит от их разности хода. Из прямоугольного треугольника АВС имеем D1-3 = АС × sin j. Здесь АВ = D1-3.
Для наблюдения максимума в точке А согласно общему условию интерференции, разность хода D1-3 должна быть равна чётному числу полуволн или целому числу длин волн:
D1-3 = 2k 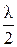 = kl,
= kl,
Так как АС = а + b, то D1-3 = (а + b) × sin j = kl. (3)
В случае дифракционной решётки a+b=d – называется периодом решетки.
Придавая "k" ряд последовательных целочисленных значений (k=0,1,2…) можно получить значение углов, в которых лежат дифракционные максимумы:
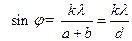 . (4)
. (4)
Для данной решётки предельно число наблюдаемых дифракционных максимумов можно найти из условия, что 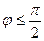 . Тогда из (3) наибольший порядок максимума, который дает данная решетка, будет:
. Тогда из (3) наибольший порядок максимума, который дает данная решетка, будет:
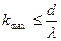 (5)
(5)
Прямая зависимость между углом дифракционного отклонения и длиной световой волны l позволяет использовать дифракционную решётку как спектральный прибор:
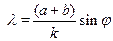 или
или 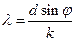 (6)
(6)
Если на решётку падает белый свет, то лучи, не претерпевшие дифракции, распространяются до и после решётки, не изменяя своего направления. Собираясь в точке Р0 (рис.5) они образуют спектр нулевого порядка, имеющий белую окраску.
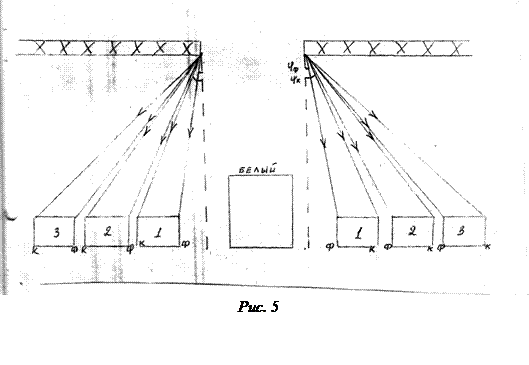 |
Лучи, испытавшие дифракционное отклонение, изменяют направление своего распространения в прямой пропорциональности к длине волны. Чем больше длина волны, тем больше отклоняется луч. Поэтому, в-первых, во-вторых и т.д. дифракционных максимумах наблюдается дифракционная окраска. В связи с ней дифракционные максимумы и получили название дифракционных спектров. Края правого и левого спектров одного порядка обращены своими фиолетовыми краями в сторону нулевого спектра. Характерной особенностью дифракционного спектра является то, что в нём спектральные области, соответствующие основным цветам спектра имеют одинаковую протяжённость.
Дата добавления: 2015-10-13; просмотров: 2206;
