Формулы комбинаторики
Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций, получаемых из элементов данного множества.
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами суммы и произведения.
Правило суммы: Если объект 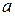 может быть выбран из совокупности объектов
может быть выбран из совокупности объектов 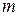 способами, и после каждого такого выбора объект
способами, и после каждого такого выбора объект 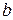 может быть выбран
может быть выбран 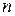 способами, то выбрать либо
способами, то выбрать либо 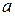 , либо
, либо 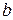 можно
можно 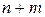 способами.
способами.
Правило произведения: Если объект 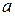 может быть выбран из совокупности объектов
может быть выбран из совокупности объектов 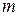 способами, и после каждого такого выбора объект
способами, и после каждого такого выбора объект 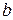 может быть выбран
может быть выбран 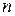 способами, то пару объектов
способами, то пару объектов 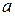 ,
, 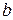 в указанном порядке можно выбрать
в указанном порядке можно выбрать 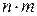 способами.
способами.
Пример 5. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Решение. По правилу произведения двух девушек можно выбрать 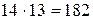 способами, а двух юношей –
способами, а двух юношей – 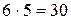 способами. Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Согласно правилу сложения число таких способов выбора будет: 182+30=212.
способами. Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Согласно правилу сложения число таких способов выбора будет: 182+30=212.
1. Перестановки.
Перестановками называют комбинации, составленные из 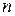 различных элементов и отличающиеся друг от друга только порядком расположения элементов.
различных элементов и отличающиеся друг от друга только порядком расположения элементов.
Число всех перестановок из 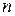 элементов вычисляется по формуле
элементов вычисляется по формуле
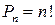
Перестановки с повторениями: если один элемент повторяется 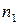 раз, второй элемент повторяется
раз, второй элемент повторяется 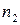 раз, к-тый элемент повторяется
раз, к-тый элемент повторяется 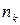 раз, а всего элементов
раз, а всего элементов 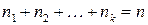 , то число комбинаций будет равно:
, то число комбинаций будет равно:
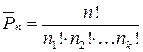 .
.
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение. Так как каждый вариант жеребьевки отличается только порядком выступления участников, то для подсчета числа различных вариантов следует воспользоваться формулой перестановок:
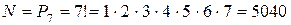 , то есть 5040 перестановок.
, то есть 5040 перестановок.
Пример. Сколько различных пятизначных чисел можно составить из цифр 3, 3, 5, 5, 8?
Решение.Каждое пятизначное число отличается только порядком следования цифр, причем цифра 3 встречается 2 раза, цифра 5 – 2 раза, а цифра 8 – 1 раз, то есть 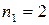 ,
, 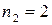 ,
, 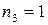 ,
, 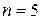 . Для подсчета числа различных пятизначных чисел следует воспользоваться формулой перестановок с повторениями:
. Для подсчета числа различных пятизначных чисел следует воспользоваться формулой перестановок с повторениями:
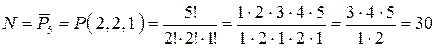 , то есть
, то есть
30 различных пятизначных цифр.
2. Размещения.
Размещениями называются комбинации, составленные из n различных элементов по 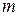 различным элементам, которые отличаются либо составом элементов, либо порядком их расположения.
различным элементам, которые отличаются либо составом элементов, либо порядком их расположения.
Число различных размещений из n элементов по 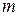 элементам определяется формулой:
элементам определяется формулой:
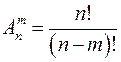 .
.
Размещения с повторениями: если каждый элемент может быть использован 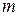 раз, то число размещений с повторениями будет равно:
раз, то число размещений с повторениями будет равно:
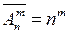 .
.
Пример. На кодовом замке 10 кнопок. Код состоит из трех различных цифр. Сколько различных кодов можно набрать?
Решение.Так как при наборе трехзначного кода можно набирать 3 цифры из имеющихся 10 в любом порядке, то есть коды могут отличаться либо составом цифр, либо порядком их расположения, то для подсчета числа различных кодов воспользуемся формулой размещений:
 , то есть
, то есть
720 различных кодов.
Пример. Пять человек вошли в лифт на первом этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
Решение.Каждый из пяти пассажиров может выйти на любом из восьми этажей со 2-го по 9-й включительно. Так как все пассажиры могут выйти на разных этажах, а могут на каком-то этаже выйти несколько пассажиров (например, на втором этаже вышел один пассажир, на четвертом – один, и трое вышли на восьмом этаже), то для подсчета числа способов выхода 5 пассажиров из лифта следует воспользоваться формулой размещения с повторениями:
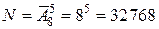 .
.
Такой же результат можно получить, используя правило умножения: для первого пассажира имеется 8 вариантов выхода на этаже, для второго тоже 8, и для третьего – 8, и для четвертого – 8, и для пятого – 8. Всего получается: 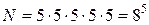 вариантов выхода 5-ти пассажиров.
вариантов выхода 5-ти пассажиров.
3. Сочетания.
Сочетаниями называются комбинации, составленные из n различных элементов по m элементам, отличающиеся друг от друга только составом элементов.
В сочетаниях, в отличие от размещений, не учитывается порядок элементов. Число сочетаний из n элементов по m элементов вычисляется по формуле
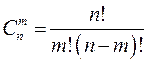 .
.
Сочетания с повторениями: если каждый элемент из n элементов может быть использован m раз, то число сочетаний с повторениями будет равно:
 .
.
Пример. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых?
Решение.Так как порядок выбора цветов не имеет значение, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно 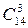 способами.
способами.
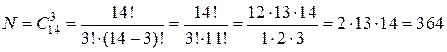 .
.
Красную гвоздику из 10 имеющихся можно выбрать 10 способами или 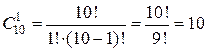 . Выбрать две розовые гвоздики из имеющихся четырех можно
. Выбрать две розовые гвоздики из имеющихся четырех можно 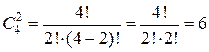 способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить (по правилу умножения)
способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить (по правилу умножения)  способами.
способами.
Пример. В магазине имеется 7 видов тортов. Сколькими способами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?
Решение.Поскольку порядок расположения тортов в наборе не играет роли, то искомое число наборов равно числу сочетаний с повторениями из 7 элементов по 3 в каждом:
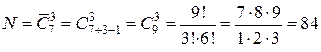 ;
;
Если имеется 3 вида тортов, а нужен набор из 7 тортов, то число возможных наборов равно:
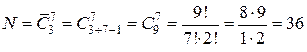 .
.
Дата добавления: 2015-10-19; просмотров: 6487;
