Урновые схемы
Есть урна, (то есть ящик), содержащая n занумерованных объектов, которые мы будем называть шариками. Мы выбираем из этой урны k шариков. Нас интересует, сколькими способами можно выбрать k шариков из n, или сколько различных результатов (то есть наборов, состоящих из k шариков) получится.
На этот вопрос нельзя дать однозначный ответ, пока мы не определимся
– с тем, как организован выбор (скажем, можно ли шарики возвращать в урну), и
– с тем, что понимается под различными результатами выбора.
Рассмотрим следующие возможные схемы выбора:
1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из k шариков выбирается из полной урны. В полученном наборе, состоящем из k номеров шариков, могут встречаться одни и те же номера (выборка с повторениями).
2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений).
И в том, и в другом случае результатом выбора является набор из k номеров шариков. Удобно считать, что шарики всегда выбираются последовательно, по одному (с возвращением или без).
Условимся, какие результаты мы будем считать различными.
Есть две возможности:
1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы (1,2,5), (2,5,1) (4,4,5) различны, если производится выбор с учетом порядка.
2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора (1,2,5), (2,5,1) есть один и тот же результат выбора, а набор (4,4,5) — другой результат выбора.
Подсчитаем теперь, сколько возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет).
Урновая схема: выбор без возвращения, с учетом порядка
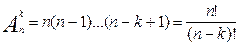 |
Общее количество выборок в схеме выбора k элементов из n без возвращения и с учетом порядка определяется числом размещений из n элементов по k элементов.
Урновая схема: выбор без возвращения и без учета порядка
 |
Общее количество выборок в схеме выбора k элементов из n без возвращения и без учета порядка определяется числом сочетаний из n элементов по k элементов:
Урновая схема: выбор с возвращением и с учетом порядка
Общее количество выборок в схеме выбора k элементов из n с возвращением и с учетом порядка определяется числом перестановок из 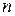 элементов:
элементов:
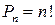
Урновая схема: выбор с возвращением и без учета порядка
Рассмотрим урну с двумя шариками и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением:
| С учетом порядка | Без учета порядка |
| (1, 1) (2, 2) (1, 2) (2, 1) | (1, 1) (2, 2) (1, 2) |
В схеме «без учета порядка» получилось 3 различных результата в отличие от четырех в схеме «с учетом порядка». Тогда общее количество выборок в схеме выбора k элементов из n с возвращением и без учета порядка определяется числом сочетаний с повторениями
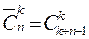 .
.
Заметим, что число выборок, различающихся еще и порядком, в k! раз больше, чем число выборок, различающихся только составом.
Пример. Рассмотрим выбор двух шариков из двух или, что то же самое, дважды подбросим монету. Если учитывать порядок, то исходов получится 4, и все они равновозможны, то есть имеют вероятность по 1/4:
(герб, герб), (решка, решка), (решка, герб), (герб, решка).
Если порядок не учитывать, то два последних исхода будут с одним и тем же результатом эксперимента, и получим три исхода вместо четырех: выпало два герба, либо две решки, либо один герб и одна решка.
При этом первые два исхода имеют вероятность 1/4, а последний — вероятность 1/4+1/4=1/2.
Дата добавления: 2015-10-19; просмотров: 4978;
