Спільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на цих прямих, перпендикулярний до кожної з них.
Доведемо, що дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, що проходять через ці прямі.
Дійсно, нехай а і b — дані мимобіжні прямі (мал. 46). Проведемо через них паралельні площини α і β. Прямі, що перетинають пряму а і перпендикулярні до площини α, лежать в одній площині (γ). Ця площина перетинає площину β по прямій а', паралельній а. Нехай В точка перетину прямих а' і b. Тоді пряма АВ, перпендикулярна до площини α, перпендикулярна і до площини β, тому що β паралельна α. Відрізок АВ — спільний перпендикуляр площин α і β, а отже, і прямих а і b.
Доведемо, що цей спільний перпендикуляр єдиний. Припустимо, що прямі а і b мають інший спільний перпендикуляр СD.
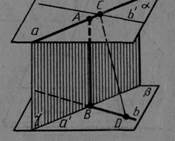 Проведемо через точку С пряму b ', паралельну b. Пряма СD перпендикулярна до прямої b, а отже, і до b'. Оскільки вона перпендикулярна до прямої а, то вона перпендикулярна і до площини α, тобто паралельна прямій АВ. Виходить, що через прямі АВ і СD, як через паралельні, можна провести площину. У цій площині будуть лежати наші мимобіжні прямі АС і ВD), а це неможливо, що й треба було довести.
Проведемо через точку С пряму b ', паралельну b. Пряма СD перпендикулярна до прямої b, а отже, і до b'. Оскільки вона перпендикулярна до прямої а, то вона перпендикулярна і до площини α, тобто паралельна прямій АВ. Виходить, що через прямі АВ і СD, як через паралельні, можна провести площину. У цій площині будуть лежати наші мимобіжні прямі АС і ВD), а це неможливо, що й треба було довести.
Мал. 46
Відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра. Вона дорівнює відстані між паралельними площинами, що проходять через ці прямі.
Дата добавления: 2015-10-19; просмотров: 1890;
