ЗАДАЧІ НА ПЕРПЕНДИКУЛЯРНІСТЬ

КОНТРОЛЬНІ ПИТАННЯ

1. Які прямі у просторі називаються перпендикулярними?

2. Доведіть, що прямі, які перетинаються і відповідно паралельні перпендикулярним прямим, перпендикулярні.

3. Дайте означення перпендикулярності прямої і площини.

4. Доведіть ознаку перпендикулярності прямої і площини.

5. Доведіть, що якщо площина перпендикулярна до однієї із двох паралельних прямих, то вона перпендикулярна і до іншої прямій.

6. Доведіть, що дві прямі, перпендикулярні до однієї і тієї ж площини, паралельні.

7. Що таке перпендикуляр, опущений з даної точки на площину?

8. Що називається відстанню від точки до площини?

9. Що таке похила, проведена з даної точки до площини? Що таке проекція похилої?

10. Доведіть теорему про три перпендикуляри.

11. Які площини називаються перпендикулярними?

12. Доведіть ознаку перпендикулярності площин.

13. Що таке спільний перпендикуляр мимобіжних прямих?

14. Доведіть, що мимобіжні прямі мають спільний перпендикуляр, і тільки один. Він є спільним перпендикуляром паралельних площин, що проходять через ці прямі.

15. Що називається відстанню між мимобіжними прямими?

ЗАДАЧІ

1. Доведіть, що через будь-яку точку прямої у просторі можна провести перпендикулярну до неї пряму.

2. Доведіть, що через будь-яку точку прямої у просторі можна провести дві різні перпендикулярні їй прямі.

3. Прямі АВ, АС і АD попарно перпендикулярні (мал. 49). Знайдіть відрізок СD, якщо: 1) АВ = 3 см, ВС = 7 см, АD = 1,5 см; 2) ВD= 9см, ВР = 16см, АD= 5см; 3) АВ = b, ВС = а, АD = d; 4) ВD = с, ВС = а, АD = АВ = d.

4* Сторони чотирикутника АВСD і прямокутника А₁В₁С₁D₁ відповідно паралельні. Доведіть, що АВСD — прямокутник.

5. Доведіть, що через точку, що не належить даній площини, не можна провести більше ніж одну пряму, перпендикулярну до площини.

6. Через центр описаного навколо трикутника кола проведену пряму, перпендикулярну до площини трикутника. Доведіть, що кожна точка цієї прямої рівновіддалена від вершин трикутника (мал. 50).

7. Через вершину А прямокутника АВСD проведена пряма АК, перпендикулярна до його площини. Відстані від точки К до інших вершин прямокутника дорівнюють 6 м, 7 м і 9 м. Знайдіть відрізок АК.

8. Через вершину гострого кута прямокутного трикутника АВС з прямим кутом С проведену пряму АD, перпендикулярну до площини трикутника. Знайдіть відстань від точки D до вершин В і С, якщо АС = а, ВС = b, АD = с.

9. Доведіть, що через дану точку прямої можна провести одну й тільки одну перпендикулярну їй площину.

10. Через точку А прямої а проведені перпендикулярні до неї площина β і пряма b. Доведіть, що пряма b лежить у площині β.

11. Доведіть, що через дану точку площини можна провести одну й тільки одну перпендикулярну їй пряму.

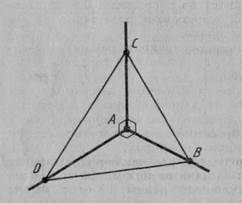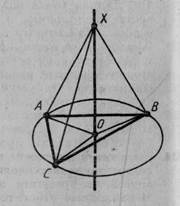Мал. 49 Мал. 50

12. Доведіть, що через будь-яку точку А можна провести пряму, перпендикулярну до даної площини α.

13. Через вершину квадрата АВСD проведена пряма ВМ, перпендикулярну до його площини. Доведіть, що: 1) пряма АD перпендикулярна до площини прямих АВ і ВМ; 2) пряма СD перпендикулярна до площини прямих ВС і ВМ.

14. Через точки А і В проведені прямі, перпендикулярні до площини α, що перетинають її в точках С і D. Знайдіть відстань між точками А і В, якщо АС = 3 м, ВD = 2 м,
СD = 2,4 м і відрізок АВ не перетинає площину α.

15. Верхні кінці двох вертикальних стовпів, що перебувають на відстані 3,4 м друг від друга, з'єднані поперечиною. Висота одного стовпа 5,8 м, а іншого 3,9 м. Знайдіть
довжину поперечини.

16. Телефонний провід завдовжки 15 м протягнуто від телефонного стовпа, де він прикріплений на висоті 8 м від поверхні землі, до будинку, де його прикріпили на висоті20м.Знайдіть відстань між будинком і стовпом, вважаючи, що провід не провисає.

17. Точка А знаходиться на відстані а від вершин рівностороннього трикутника зі стороною а. Знайдіть відстань від точки А до площини трикутника.

18. З точки S поза площиною α проведені до неї три різні похилі SА, SВ, SС і перпендикуляр SО. Доведіть, що основа перпендикуляра О є центром кола, описаного навколо трикутника АВС.

19. Сторони рівностороннього трикутника дорівнюють 3 м. Знайдіть відстань до площини цього трикутника від точки, віддаленої від кожної з його вершин на 2 м.

20.* У рівнобедреному трикутнику основа і висота рівні 4 м. Дана точка знаходиться на відстані 6 м від площини трикутника і на однаковій відстані від його вершин. Знайдіть цю відстань.

21. Відстані від точки А до вершин квадрата дорівнюють а. Знайдіть відстань від точки А до площини квадрата, якщо сторона квадрата рівна b.

22. Знайдіть геометричне місце основ похилих даної довжини, проведених з даної точки до площини.

23. З точки до площини проведено дві похилі, рівні 10 см і 17 см. Різниця проекцій цих похилих становить 9 см. Знайдіть проекції похилих.

24. З точки до площини проведено дві похилі. Знайдіть довжини похилих, якщо: 1) одна з них на 26 см більше за іншу, а проекції похилих рівні 12 см і 40 см;
2) похилі відносяться, як 1:2, а проекції похилих рівні 1 см і 7 см.

25. З точки до площини проведено дві похилі, рівні 23 см і 33 см. Знайдіть відстань від цієї точки до площини, якщо проекції похилих відносяться, як 2:3.

26. Доведіть, що якщо пряма паралельна площини, усі її точки перебувають на однаковій відстані від площини.

27. Через вершину прямого кута С прямокутного трикутника АВС проведена площина, паралельна гіпотенузі, на відстані 1 м від неї. Проекції катетів на цю площину рівні 3 м і 5 м. Знайдіть гіпотенузу.

28. Через одну сторону ромба проведено площину на відстані 4 м від протилежної сторони. Проекції діагоналей на цю площину рівні 8 м і 2 м. Знайдіть проекції
сторін.

29. З кінців відрізка АВ, паралельного площині, проведені перпендикуляр АС і похила ВD, перпендикулярна відрізку АВ (мал. 51). Чому дорівнює відстань СD, якщо АВ = а, АС = b, ВD = с.

30. Доведіть, що відстані від усіх точок площини до паралельної площини однакові.

31. Відстань між двома паралельними площинами дорівнює а. Відрізок довжиною b своїми кінцями упирається в ці площини. Знайдіть проекцію відрізка на кожну із
площин.

32. Два відрізки довжин а і b упираються кінцями у дві паралельні площини. Проекція першого відрізка (довжини а) на площину дорівнює с. Знайдіть проекцію другого відрізка.

33. Кінці даного відрізка, що не перетинає площину, віддалені від неї на 0,3 м і 0,5 м. Як віддалена від площини точка, що ділить даний відрізок у відношенні 3:7?

34. Через середину відрізка проведено площину. Доведіть, що кінці відрізка знаходяться на однаковій відстані від цієї площини.

35. Через діагональ паралелограма проведена площина. Доведіть, що кінці іншої діагоналі знаходяться на однаковій відстані від цієї площини.

36. Знайдіть відстань від середини відрізка АВ до площини, що не перетинає цей відрізок, якщо відстані від точок А і В до площини дорівнюють: 1) 3,2 см і 5,3 см; 2) 7,4 см і 6,1 см; 3) а і b.

37. Розв'яжіть попередню задачу, уважаючи, що відрізок АВ перетинає площину.

38. Кінці відрізка довжиною 1 м віддалені від площини, яку він перетинає, на 0,5 м і 0,3 м. Знайдіть довжину проекції відрізка на площину.

39. Через основу трапеції проведена площина на відстані а від іншої основи. Знайдіть відстань від точки перетину діагоналей трапеції до цієї площини, якщо основи трапеції відносяться, як m:n (мал. 52).

40. Через сторону паралелограма проведена площина на відстані а від протилежної сторони. Знайдіть відстань від точки перетинання діагоналей паралелограма до цієї площини.

41. З вершини квадрата проведено перпендикуляр до його площини. Відстані від кінця цього перпендикуляра до інших вершин квадрата дорівнюють а і b (а< b). Знайдіть довжину перпендикуляра і сторону квадрата (мал. 53).

42. З вершини прямокутника проведено перпендикуляр до його площини. Відстані від кінця цього перпендикуляра до інших вершин прямокутника рівні а, b, с (а<с, b <с).
Знайдіть довжину перпендикуляра і сторони прямокутника.

43. З даної точки до площини проведено дві рівні похилі довжиною 2 м. Знайдіть відстань від точки до площини, якщо похилі утворюють між собою кут 60^о, а їх проекції перпендикулярні.

44. З точки, що віддаленої від площини на відстань 1 м, проведено дві рівні похилі. Знайдіть відстань між основами похилих, якщо відомо, що похилі перпендикулярні і утворюють із перпендикуляром до площини кути рівні 60°.

45. Через центр вписаного в трикутник кола проведена пряма, перпендикулярна до площини трикутника. Доведіть, що кожна точка цієї прямої рівновіддалена від сторін трикутника.

46. До площини трикутника з центра вписаного у нього кола радіуса 0,7 м проведено перпендикуляр довжиною 2,4 м. Знайдіть відстань від кінця цього перпендикуляра до сторін трикутника.

47. Відстань від даної точки до площини трикутника дорівнює 1,1 м, а до кожної з його сторін 6,1 м. Знайдіть радіус кола, вписаного в цей трикутник.

48. З вершини рівностороннього трикутника АВС проведено перпендикуляр АD до площини трикутника. Знайдіть відстань від точки D до сторони ВС, якщо АD = 13 см, ВС = 6 см.

49. Через кінець А відрізка АВ довжиною b проведена площина, перпендикулярну до відрізка, і в цій площині проведено пряму. Знайдіть відстань від точки В до прямої, якщо відстань від точки А до прямої дорівнює а.

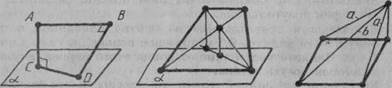Мал. 51 Мал. 52 Мал. 53

50. Відстані від точки А до всіх сторін квадрата дорівнює а. Знайдіть відстань від точки А до площини квадрата, якщо діагональ квадрата дорівнює d.

51. Точка М, що лежить поза площиною даного прямого кута, віддалена від вершини кута на відстань а, а від його сторін на відстань b. Знайдіть відстань від точки М до площини кута.

52.* Даний рівнобедрений трикутник з основою 6 м і бічною стороною 5 м. Із центру вписаного в нього кола проведено перпендикуляр до площини трикутника довжиною 2 м. Знайдіть відстань від кінця цього перпендикуляра до сторін трикутника.

53. З вершини прямого кута С трикутника АВС проведено перпендикуляр СD до площини трикутника. Знайдіть відстань від точки D до гіпотенузи трикутника, якщо АВ = а, ВС = b, СD = с.

54. Дані пряма c і площина α . Проведіть через пряму а площину, перпендикулярну до площини α.

55. Дано пряму а і площину α. Доведіть, що всі прямі, перпендикулярні до площини α і перетинають пряму а, лежать в одній площині, перпендикулярній до площини α.

56. З вершин А і В рівностороннього трикутника АВС проведені перпендикуляри АА₁ і ВВ₁ до площини трикутника. Знайдіть відстань від вершини С до середини
відрізка А₁В₁, якщо АВ = 2 м, СА₁ =3 м, СВ₁ =7 м і відрізок А₁В₁ не перетинає площину трикутника.

57. З вершин А і В гострих кутів прямокутного трикутника АВС проведені перпендикуляри АА₁ і ВВ₁ до площини трикутника. Знайдіть відстань від вершини С до середини відрізка А₁В₁, якщо А₁С = 4 м, А₁А = 3 м, В₁С = 6 м, В₁В = 2 м і відрізок А₁В₁не перетинає площину трикутника.

58. З точок А і В, що лежать у двох перпендикулярних площинах, опущені перпендикуляри АС і ВD на пряму перетинання площин. Знайдіть довжину відрізка АВ, якщо: 1) АС = 6м, ВD = 7м, СD = 6м; 2) АС = 3м, ВD=4м, СD =12м; 3) АD = 4м, ВС= 7м, СD = 1м; 4) АD=ВР = 5м, СD = 1м; 5) АС = а, ВВ = b, СD = з; 6) АD = а, ВС = b, СD = с.

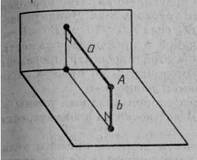
59. Точка знаходиться на відстанях а і b від двох перпендикулярних площин. Знайдіть відстань від цієї точки до прямій перетинання площин (мал. 54).

60. Площини аіβ перпендикулярні. У площині α взята точка А, відстань від якої до прямої с (лінії перетинання площин) дорівнює 0,5 м. У площині β проведена пряма b, паралельна прямій с і віддалена від неї на 1,2 м. Знайдіть відстань від точки А до прямій b.

61. Перпендикулярні площини аіβ перетинаються по прямій с. У площині а проведена пряма а ‌|| с, а в площині β — пряма b || с. Знайдіть відстань між прямими а і b, якщо відстань між прямими b і с дорівнює 1,5 м, а між прямими b і с — 0,8 м (мал. 55).

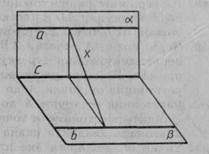Мал. 54 Мал. 55