Ознака перпендикулярності площин

Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетинання цих площин, перетинає їх по перпендикулярних прямих.

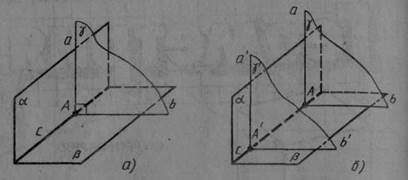
На малюнку 44, а ви бачите дві перпендикулярні площини α і β, що перетинаються по прямій с. Площина γ, перпендикулярна до прямої с, перетинає площини α і β по перпендикулярним прямим а і b.

Будь-яка площина, перпендикулярна до лінії перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих.

Дійсно, якщо взяти іншу площину γ', перпендикулярну до прямої с, то вона перетне площину α по прямій а', перпендикулярній до с, а виходить, паралельній прямій а, а площину β — по прямій b', перпендикулярній до с, отже, паралельній прямій b (мал. 44, б). За теоремою 3.1 з перпендикулярності прямих а і b випливає перпендикулярність прямих а' і b', що й було потрібно довести.

Теорема 3.6. Якщо площина проходить через пряму, перпендикулярну до другої площини, те ці площини перпендикулярні.

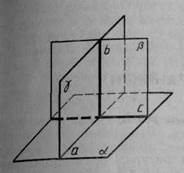
Доведення. Нехай α — площина, b — пряма, перпендикулярна до цієї площини, β — площина, що проходить через пряму b, і с — пряма, по якій перетинаються площини α і β (мал. 45). Доведемо, що площини α і β перпендикулярні.

Проведемо в площині α через точку перетину прямої b з площиною α пряму а, перпендикулярну до прямої с. Проведемо через прямі а і b площина γ. Вона перпендикулярна до прямої с, тому що пряма с перпендикулярна до прямих а і b. Оскільки прямі а і b перпендикулярні, то площини α і β також перпендикулярні. Теорема доведена.

 

Мал. 44 Мал. 45

 

<13141516171819>

---

Дата добавления: 2015-10-19; просмотров: 3591;

---