Синтез кулачкового механизма с качающимся

роликовым толкателем(рисунок 4.1, г)

Исходные данные. Линейно - убывающий закон движения толкателя (диаграмма аналога ускорения, рисунок 4.15); фазовые углы φ_у, φ_дс, φ_п, причем φ_у = φ_п; угол давления J; длина толкателя ℓ_СЕ; угловая скорость кулачка ω₁, β_maxёёё – угловое перемещение толкателя.

Определить: ℓ_Rо, ℓ_rрол и построить профиль кулачка.

Решение. Построение диаграмм ведется аналогично п. 4.1.5, только вместо диаграммы аналога ускорения d²S/dφ² будет график аналога углового ускорения d²β/dφ², Вместо аналога скорости dS/dφ будет график аналога угловой скорости dβ/dφ, вместо диаграммы перемещения S будет график углового перемещения толкателя β_max. Тогда масштабные коэффициенты диаграмм будут рассчитываться по формулам:

μ_β=β_max/h_max= (рад/мм);

μ_dβ/dφ= μ_β/Н₂μ_φ=(1/мм); (4.13)

μd²β/dφ²= μ_dβ/dφ/Н₁μ_φ=(рад^-1/мм),

где угловое перемещение в радианах β_max=π β_max/180⁰ = (рад), Н₁ и Н₂ – полюсные расстояния в мм. Масштабные коэффициенты угловых скоростей и ускорений рассчитываются по формулам:

μ_ω=μ_β/H₂μ_t= μ_dβ/dφ ω₁= (рад с^-1/мм);

μ_ξ =μ_ω/H₁μ_t= μd²β/dφ² ω²₁ = (рад с^-2/мм). (4.14)

Для определения минимального радиуса кулачка высчитывается масштабный коэффициент длины μ_ℓ = ℓ_АВ/АВ =(м/мм). На свободном поле чертежа отмечается т. Е и откладывается угол β_max (рисунок 4.18, а). Проводится дуга радиусом, равным длине толкателя ВЕ. Затем откладываются отрезкии отмечаются точки [В₁В₂], [В₁В₃], [В₁В₄] равные высотам h₁, h₂ h₃, h₄, взятым с диаграммы углового перемещения толкателя. Точки В₁, В₂, В₃, В₄ соединяются с точкой Е. На полученных лучах откладываются отрезки [В₂С₂], [В₃С₃], [В₄С₄], равные высотам h^΄₁, h^΄₂, h^΄₃, h^΄₄, взятым с диаграммы угловой скорости. Точки С₁, С₂, С₃, С₄, С₅ соединяем плавной линией.

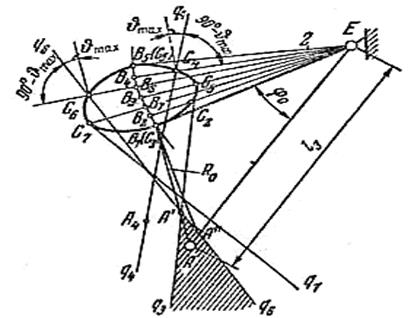
Рисунок 4.18, а - Графическое определение минимального радиуса

кулачка с качающимся роликовым толкателем

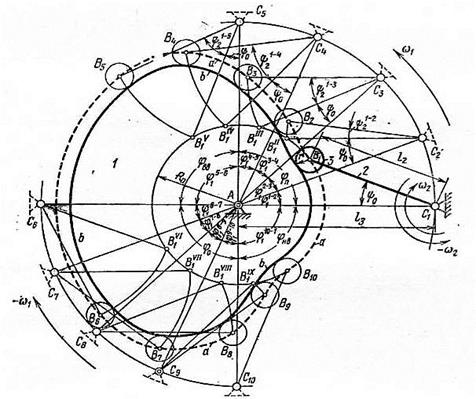
Рисунок 4.18, б - Построение профиля кулачка с качающимся толкателем

Получаем диаграмму β-dβ/dφ. Из этих точек проводим лучи q₁, q₂, q₃, q₄ под углом передачи γ = 90^о - J. Наиболее удаленная точка пересечения этих лучей будет являться центром вращения кулачка – т.А'. Из конструктивных соображений выбираем за центр вращения кулачка точку А, которая будет лежать в области допустимых значений. Тогда отрезок [AВ₁] является минимальным радиусом кулачка R_о. Действительное значение минимального радиуса находится по формуле ℓ_Rо=[AВ₁]μ_ℓ=(м). Из построения определяться начальный угол φ_о и межосевое расстояние ℓ₃=[AE].

Построение профиля кулачка с качающимся толкателем. Из произвольно выбранной точки А строим окружности радиусами ℓ₃=[AE] и r_o (рисунок 4.18, б). На окружности радиусом ℓ₃ выбираем в произвольном месте точку C₁. От этой точки откладываем отрезок ℓ₂=[В₁С₁], где ВС – длина толкателя. От межосевого расстояния АС₁ в противоположную сторону вращения кулачка откладываем углы φ_у, φ_дс, φ_п, которые делим на равные четыре части. На окружности радиусом ℓ₃ отмечаем точки С₁, С₂, С₃, С₄, С₅. Из этих точек проводим дуги радиусом ℓ₂=[В₁С₁] – отмечаем точки 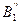, , 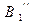, 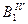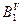. На соответствующих дугах от полученных точек откладываем отрезки, равные высотам диаграммы углового перемещения h₁, h₂ h₃, h₄. Точки В₁, В₂, В₃, В₄, В₅ соединяем плавной линией - получаем теоретический профиль кулачка с качающимся роликовым толкателем. Практический профиль строится аналогично п. 4.1.5.