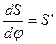Синтез кулачкового механизма с центральным

роликовым толкателем (рисунок 4.1, а)

Исходные данные. Линейно - убывающий закон движения толкателя (диаграмма аналога ускорения); фазовые углы φ_у, φ_дс, φ_п, причем φ_у = φ_п; угол давления J; ход толкателя ℓ_hmax; угловая скорость кулачка ω₁.

Определить: ℓ_Rоmin, ℓ_rрол и построить профиль кулачка.

Решение. Построение кинематических диаграмм. Начинаем с построения диаграммы аналога ускорения (рисунок 4.15).

d²S/dφ²

а₁ а₂

Р₁

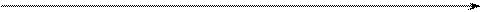
0 1 2 3 4 5 6 7 8 9 φ

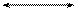
Н₁

dS/dφ

Р₂

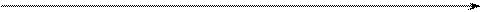Н₂ 0 1 2 3 4 5 6 7 8 9 φ

S

h_max

0 1 2 3 4 5 6 7 8 9 φ

φ_у φ_дс φ_п

Рисунок 4.15 - Построение диаграмм аналогов ускорения, скорости и

перемещения методом графического интегрирования

Для этого произвольно выбираем амплитуду а₁. Если φ_у = φ_п (по заданию это так), то а₁= а_2. Если же φ_у ≠ φ_п, то амплитуду а₁ выбираем произвольно, а амплитуда а₂ определится из пропорции:

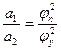, (4.4)

где φ₁ и φ₃ – заданные фазовые углы в градусах, а₁ и а₂ – амплитуды в мм.

Чтобы определить расстояния φ_у, φ_дс и φ_п в мм, необходимо посчитать масштабный коэффициент угла μ_φ:

μ_φ = φ_раб/[0-9] = (рад/мм), (4.5)

где [0-9] – произвольно выбранный отрезок на оси φ. Угол φ_раб в градусах высчитывается по формуле (4.1). Чтобы подставить его значение в формулу (4.5), нужно выполнить перерасчет в радианы

φ_раб = φ^о_рабπ/180 = (рад). (4.6)

Пересчитываем каждый угол в радианы по формуле (4.6) и находим каждое значение в мм:

[φ_у] = φ_у/μ_φ, [φ_дс] = φ_дс/μ_φ, [φ_п] = φ_п/μ_φ= (мм). (4.7)

Откладываем полученные значения по оси φ, выбираем произвольно амплитуду а₁ и строим заданную диаграмму аналога ускорения (рисунок 4.15).

Начинаем построение диаграммы аналога скорости методом графического интегрирования. Как указывалось в главе 2, §2.4, п.2.4.3 этот метод является обратным методу графического дифференцирования. Поэтому, при выборе полюсного расстояния Н нужно руководствоваться следующим определением: чем больше полюсное расстояние, тем положе будет график аналога скорости. Итак, с левой стороны графика аналога ускорения выбираем полюсное расстояние Н₁. Каждый участок на оси φ, т.е. отрезки [0÷1], [1÷2], [2÷3] и т.д., делим пополам. Проводим вертикальные линии до соединения с графиком, затем горизонтальные с осью d²S/dφ² и соединяем с точкой полюса Р₁. Затем полученные линии параллельно переносим на соответствующие участки на диаграмме аналога скорости dS/dφ. Аналогично строим график перемещения S. На диаграмме перемещения отмечаем наибольшую высоту h_max - ход толкателя в мм.

После построения диаграмм высчитываем масштабные коэффициенты графиков. Т.к. задан ход движения толкателя, то расчет масштабных коэффициентов ведется по методу графического дифференцирования

μ_S= ℓ_hmax/h_max = (м/мм);

μdS/dφ = μ_S/(H₂μ_φ) = (^мрад-1/_мм); (4.8)

μd²S/dφ² = μdS/dφ/(H₁μ_φ) = (^мрад-2/_мм),

где Н₁ и Н₂ – полюсные расстояния в мм.

Рассчитаем масштабные коэффициенты графиков через время

t_раб = φ_раб/ω_К; μ_t = t_раб/[0-9] =(с/мм);

μ_V = μ_S/(H₂μ_t) = (^м/с/_мм); (4.9)

μ_a= μ_V/(H₁μ_t) = (^м/с2/_мм).

Определение минимального радиуса кулачка ℓ_Rо графическим методом. Строим диаграмму зависимости аналога скорости от перемещения 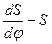, исключая параметр φ (рисунок 4.16, а). Для этого проводим кривую как для фазы подъема, так и для фазы опускания. Далее проводим к полученной кривой касательные t₁-t₁ и t₂-t₂ под углами J к оси S₂. Точка А' пересечения этих касательных определит положение центра вращения кулачка, имеющего наименьший радиус-вектор R_оmin.

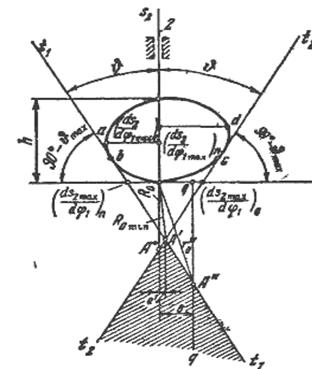
Действительное значение минимального радиуса определится по формуле:

ℓ_Rо=R_оμ_ℓ=(м). (4.10)

Заштрихованная область будет являться геометрическим местом точек центра вращения кулачка. Отметим, что точки касания b и c касательных t₁-t₁ и t₂-t₂ с кривой 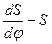не совпадают с точками a и d.

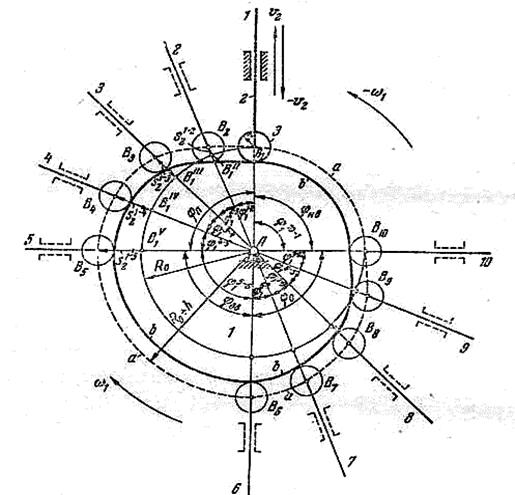
Рисунок 4.16, б - Профилирование кулачка с центральным

роликовым толкателем

Начинаем профилирование кулачка (рисунок 4.16, б). Построение профиля можно проводить в том же масштабе, в котором определялся минимальный радиус. Если же получается очень мелкое или, наоборот, крупное изображение, то выполняют перерасчет масштабного коэффициента:

μ^΄_ℓ=ℓ_Rо/[R_о]=(м/мм), (4.11)

где [R_о]-произвольно выбранный радиус кулачка.

При профилировании кулачка применяется метод обращения движения. Для этого мысленно придаем всему механизму вращение вокруг центра А с угловой скоростью ω = -ω_К. Тогда угловая скорость кулачка становится равной ω_К+(-ω_К)=0, т.е. кулачок становится неподвижным, а толкатель приобретает вращение относительно центра А. Практически это делается так. Из произвольно выбранной точки А, проводим окружность радиусом R_о (рисунок 4.16, б). Отмечаем точку В₁, которую соединяем с точкой А. От вертикальной оси [АВ₁] в противоположную сторону вращения друг за другом откладываем углы φ_у, φ_дс и φ_п. Делим углы φ_у и φ_п на равные части, согласно делению на диаграмме (в данном примере на 4). Получаем точки 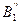, , 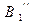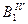и т.д., через которые из точки А проводим лучи 2, 3, 4 и т.д. 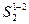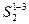От этих точек откладываем отрезки =h₁, =h₂, 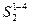=h₃ и т.д. на лучах 2, 3, 4 соответственно, взятые с диаграммы перемещения. Получаем точки В₂, В₃, В₄. Полученные точки соединяем между собой и с точкой В₁. Получаем теоретический профиль кулачка – эквидистанту. Для построения практического профиля кулачка, необходимо посчитать радиус ролика, т.к. точки В₁, В₂, В₃, В₄ и т.д. будут являться центрами ролика. Радиус ролика выбирается как минимальное значение из двух уравнений:

ℓ_rрол < 0,8ρ_min

ℓ_rрол < [0,4…0,5]ℓ_Rо, (4.12)

где ρ_min- минимальный радиус кривизны профиля. Практический профиль строится как огибающая кривая положений ролика.