Синтез кулачкового механизма со смещенным
роликовым толкателем (с эксцентриситетом)(рисунок 4.1, б)
Исходные данные. Линейно - убывающий закон движения толкателя (диаграмма аналога ускорения, рисунок 4.15); фазовые углы φу, φдс, φп, причем φу=φп; угол давления J; ход толкателя ℓhmax; угловая скорость кулачка ω1, эксцентриситет ℓе.
Определить: ℓRоmin, ℓrрол и построить профиль кулачка.
Решение. Построение диаграмм, расчет масштабных коэффициентов графиков проводится аналогично п. 4.1.5. Чтобы определить минимальный радиус кулачка со смещением, необходимо определить радиус кулачка без смещения (п. 4.1.6). Далее выполняют следующие построения. От вертикали [Аs2] вправо откладываем смещение оси движения толкателя - эксцентриситет е (рисунок 4.16, а), чертежное значение которого рассчитываем по формуле
е =ℓе/μℓ=(мм).
Проводим вертикальную линию до пересечения с областью допустимых значений центров вращения кулачка. Полученная точка А'' будет являться центром вращения кулачка со смещенным толкателем. Минимальным радиусом будет являться отрезок 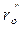 . Действительное значение радиуса определится по формуле:
. Действительное значение радиуса определится по формуле:
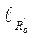 =
= 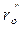 μℓ = (м).
μℓ = (м).
Строим профиль кулачка со смещенным толкателем (рисунок 4.17).
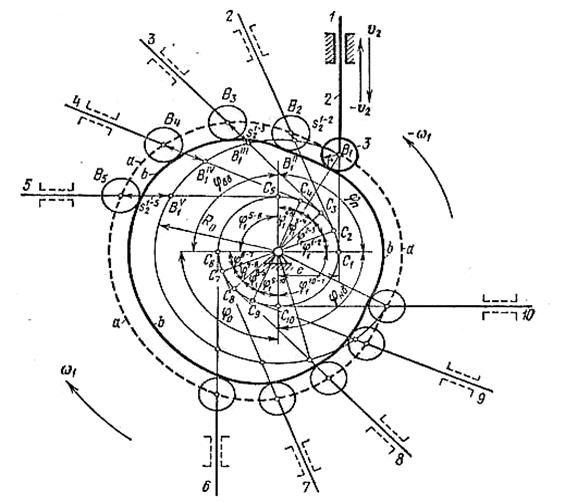
Рисунок. 4.17 - Построение профиля кулачка со смещенным толкателем
Рассчитываем масштабный коэффициент μ΄ℓ по формуле (4.11). Из произвольно выбранной точки А проводим окружности радиусами ro и е. Справа от окружности е проводим линию, касательную к ней. Получаем точку C1. На окружности радиусом 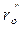 отмечаем точку В1, которая соответствует начальному положению толкателя. Затем в противоположную сторону вращения кулачка откладываем углы φу, φдс и φп. Делим углы φу и φп на равные части согласно диаграмме. Отмечаем точки С2, С3, С4 и т.д. и проводим из них касательные 1, 2, 3, 4 к окружности радиуса е. На пересечении этих касательных с окружностью радиусом ro отмечаем точки
отмечаем точку В1, которая соответствует начальному положению толкателя. Затем в противоположную сторону вращения кулачка откладываем углы φу, φдс и φп. Делим углы φу и φп на равные части согласно диаграмме. Отмечаем точки С2, С3, С4 и т.д. и проводим из них касательные 1, 2, 3, 4 к окружности радиуса е. На пересечении этих касательных с окружностью радиусом ro отмечаем точки 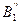 ,
, 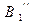 ,
, 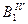 . От этих точек на соответствующих касательных откладываем отрезки
. От этих точек на соответствующих касательных откладываем отрезки 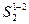 =h1,
=h1, 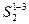 =h2,
=h2, 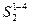 =h3, взятые с диаграммы перемещения. Получаем точки В2, В3, В4 и т.д., которые соединяем плавной линией. Получаем теоретический профиль кулачка. Практический профиль строится аналогично пункту 4.1.5.
=h3, взятые с диаграммы перемещения. Получаем точки В2, В3, В4 и т.д., которые соединяем плавной линией. Получаем теоретический профиль кулачка. Практический профиль строится аналогично пункту 4.1.5.
Дата добавления: 2015-10-19; просмотров: 1532;
