Контурлық токтар әдісі

Контурлық токтар әдісінде, схеманың әрбір тәуелсіз контурда, өзінің контурлық тогы жүруге тиіс деп есептейді. Контурлық токтарға салыстырып, теңдеулер құрады да, сонан кейін контурлық контур арқылы тармақтардағы токтар анықталады.

Сонымен, контурлық токтар әдісі ізделініп отырған шама үшін контурлық ток қабылданатын есептеу әдісі ретінде анықталады. Бұл әдістегі белгісіздердің саны, схема үшін Кирхгофтың екінші заңы бойынша құралуға тиісті теңдеулер санына тең болуы керек.

Демек, есептеу жұмыстарында контурлық токтар әдісі, Кирхгоф заңына негізделген әдіске (мұнда теңдеулер саны аз болады) қарағанда, өте тиімді (үнемді).

Енді 8 суретіндегі схемадағы екі тәуелсіз контурларға байланысты негізгі есептік теңдеулерді құру жолын қарастырамыз. Сол жақ контурда сағат тілі бағытында I₁₁ - тогы жүріп жатыр деп есептейік. Ал оң жақ контурда сондай бағытта I₂₂ - тогы жүрсін. Әрбір контур үшін Кирхгофтың 2-ші заңы бойынша теңдеулер құрамыз. Бұл жағыдайда, іргелес (кедергісі R₅) тармақта жоғарыдан төмен қарай (I₁₁ - I₂₂) тогы жүретінін ескереміз. 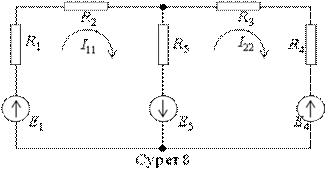Контурды айналып өтуді сағат тілі бағытында болып деп қабылдаймыз.

Бірінші контур үшін

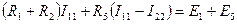(11)

немесе мұны былайша жазамыз:

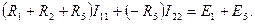(12)

Екінші контур үшін

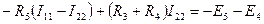(13)

немесе мұны мына түрде жазамыз:

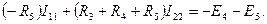(14)

Бірінші контур (12) теңдеудегі І₁₁ көбеіткіш алдында тұрған кедергілердің қосындысын R₁₁ деп белгілеп, ал (12) теңдеуіндегі І₂₂ - тогының (іргелес тармақтың кедергісі минус таңбасымен алынған) кедергісін - R₁₂ деп белгілейміз де, жоғарыдағы теңдеулерді қайта жазамыз:

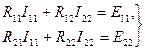(15)

Мұндағы

R₁₁ = R₁ + R₂ + R₅; E₁₁ = E₁ + E₅; R₁₂ = R₂₁ = - R₅; R₂₂ = R₃ + R₄ + R₅;

E₂₂ = - E₄ - E₅,

бұл белгілеулердегі R₁₁ - бірінші контурдың толық немесе өзіндік кедергісі; R₁₂ - бірінші және екінші контурлар арасындағы іргелес тармақтардың минус таңбасымен алынған кедергісі; Е₁₁ - бірінші контурдың э.қ.к-і, ол осы контурдың э.қ.к-нің алгебралық қосындысына тең (онда э.қ.к-нің таңбасы контурды айналып өту бағытымен сәйкес келген жағдайда алынған); R₂₂ - екінші контурдың толық немесе өзіндік кедергісі; R₂₁ - минус таңбасымен алынған, бірінші және екінші тармақтар арасындағы іргелес тармақтардың кедергісі; E₂₂ - екінші контурдың контурлық э.қ.к-і.

* Жалпы жағдайда k - және m - контурларының арасында іргелес тармақтағы теңдеуге кіретін (R_km) кедергінің таңбасы минус болуы тармақтағы контурлық I_kk - және I_mm - токтарының бағыттары қарама-қарсы болған жағдайда өтеді, ал егер бұл токтардың бағыттары бір-біріне сәйкес келсе, онда кедергі оң таңбамен алынады.

Егер схемада контурлар саны екіден көп болса, мысалы үшеу болса, онда теңдеулер жүйесі мынадай түрде болады:

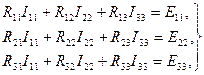(16)

немесе матрицалық түрде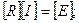

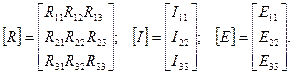(17)

Әр түрлі индексті кедергілірдегі таңбалар біркелкі болу үшін контурлық токтарды бір бағытқа бағыттау керек, яғни мысал үшін ол сағат тілінің айналу бағыты болғаны дұрыс деп ұсынылады.

Теңдеулер жүйесін шешу барысында, бір немесе бірнеше контурлық токтардың таңбалары теріс болуы мүмкін.

Екі көршілес контурлардың арасы (мысалы 8 - суретіндегі схемадағы тармақтағы R₁ - және R₂ - кедергілер) іргелес болмаған жағдайдағы тармақтардағы табылған контурлық ток тармақтың нақты тогы болады.

Іргелес тармақтардың контурлық токтар арқылы тармақтың токтарды анықтайды. Мысалы, R₅ - кедергісі бар тармақ арқылы жоғарыдан төмен қарай жүретін токтардың айырымы I₁₁ - I₂₂.

Егер электр тізбегінде п тәуелсіз контурлар болса, онда теңдеулер саны да п болады.

Сонымен п - теңдеулер жүйесінің І_kk - токпен салыстырғандағы жалпы шешуі мынадай болады:

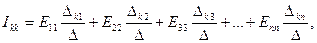(18)

мұндағы 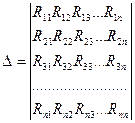- жүйенің анықтаушы.

∆_km - нің алгебралық толықтырмасы ∆ - анықтаушынан k - шы бағананы және m - ші жолды сызып тастау арқылы және сол алынған анықтаушты (-1)^k+m - не көбейту арқылы алынған.

Егер анықтауыштың жоғарғы сол жақ шеткі бұрышынан оның оң жақ төменгі бұрышына (бас диагональ) диагональ жүргізсек және R_km = R_mk теңдігін ескерсек, онда анықтауыштың екі бөлікке бөлініп, айнадағы кескін секілді олар бірін-бірі қайталайтына көз жеткізуге болады. Анықтауыштың осындай қасиетін бас диагональға салыстырғандағы симметрия деп айтады. Анықтауыштың бас диагональға қатысты симметриясына байланысты ∆_km = ∆_mk теңдігі орындалады.