Бұтақ және шекара әдісі туралы қысқаша түсінік
Бүтін санды есептерді шешуге қазіргі кезге дейін сан түрлі әдістемелер жасалынғаныменен, олардың біреуі де тиімді есептеу процедураларымен қамтамасыз етілген жоқ. Мұндай жағдайлар есептің өлшемі үлкейген сайын ерекше сезіледі, тіпті үлкен қателіктер жіберіледі.
Сонымен, сызықты программалау есептеріне қарағанда бүтін санды программалау есептерін шешу алгоритмдерін компьютермен орындаған кезде біраз қиындықтар кездеседі. Осы қиындықтарды шешумен бүгінгі күнге дейін көптеген жас зерттеушілер айна-ласуда. Олар бүтін санды есептерді шығаруға біраз әдістерді жасап та тастады. Солардың ішінде компьютер тілінде орындауға әжептәуір қызықты және ыңғайлы алгоритм, ол “Бұтақ және шекара” әдісінің алгоритмі. Бұл әдістің алгоритмін ұсынған А. Лэнд және А. Дайг.
Қарастырылып отырған әдістің негізгі идеясы – іздеп отырған шешімді тапқанынша бастапқы көптікті бірінен кейін бірін, бірнеше ішкі көптікке, яғни бұтақтан бұтаққа бөліп, жаңа есептер құрылады да, олардың шешімдерін, яғни барлық ішкі көптіктерде шешімдерді іздейді.
Оңтайлы бүтін санды шешімі табылған көптік бұтақтарға бөлінбейді, оған ақырғы немесе ілініп тұрған бұтақтың ұшының төбесі сәйкес келеді.
Бұл әдіспен есепті шығару үрдісі, Гомори әдісіндегі кесіп тастайтын жазықтар сияқты үздіксіз сызықты программалау есебін шығарудан басталады.
Бір мысал қарастырайық. Мысал, көлемі 20 мың ө.б. (өлшем бірлігі) А және көлемі 38 мың ө.б. Б шикі заттарынан екі түрлі бұйымдар жасалмақшы. Нарықта бірінші бұйымның бір данасын 7 мың теңгеге, ал екінші бұйымның бір данасын 3 мың теңгеге өткізуге болады. Әрбір бұйымның бір данасына, сәйкесінше: А шикі заттынан – (5 және 2) мың ө.б., Б шикі заттынан – (8 және 4) мың ө.б. мөлшерде жұмсалынуға тиісті. Жасалған бұйымдарды нарыққа өткізу арқылы максимальды табыс алу үшін, өндіріс орынына оларды қанша данадан өндірген тиімді.
Шешімі. Бұйымдардың оңтайлы өндіру санын, сәйкесінше x1 және x2 деп белгілеп, есептің математикалық моделін құрамыз (1-ші есеп):
Z = 7x1 + 3x2 ® max
5х1 + 2х2 £ 20,
8х1 + 4х2 £ 38,
x1³ 0, x2 ³ 0 және x1, x2 – бүтін сандар.
Ізделініп отырған айнымалылардың мәні бүтін сан болу шарттын алып тастап, кәдімгі симплекс әдісімен оңтайлы шешімді табылды: х1
|
|
Шешімде х2
|
|
x2≤7 және x2≥8
Нәтижесінде, 2-ші есеп.
Z = 7x1 + 3x2 ® max
5х1 + 2х2 £ 20
8х1 + 4х2 £ 38
х2 £ 7
x1³ 0 және х2³ 0.
Симплекс әдісімен шығару нәтижесінде: х1
|
|
Әрі қарай х1
|
Z = 7x1 + 3x2 ® max
5х1 + 2х2 £ 20
8х1 + 4х2 £ 38
х2 ³ 8
x1³ 0 және х2³ 0
Симплекс әдісімен шығару нәтижесінде: х1
|
|
Шешімде х
|
4-ші есеп. Z = 7x1 + 3x2 ® max
5х1 + 2х2 £ 20,
8х1 + 4х2 £ 38,
х1 £ 1 және х2 £ 7,
x1³ 0 және х2³ 0.
Симплекс әдісімен шығару нәтижесінде: х1
|
|
5-ші есеп. Z = 7x1 + 3x2 ® max
5х1 + 2х2 £ 20,
8х1 + 4х2 £ 38,
х1 ≥ 2 және х2 £ 7,
x1³ 0 және х2³ 0.
Симплекс әдісімен шығару нәтижесінде: х1
|
|
Сонымен, жоғарыдағы есептердің шешімі бойынша 2.1-кестені тұрғызайық.
2.1-кесте
| Көрсеткіштер | Есептер | ||||
| X1 | 1,2 | 0,75 | |||
| X2 | 7,5 | ||||
| Z | 29,5 | 29,4 | 29,25 |
Кестеден көріп отырмыз, 4-ші есептің шешімі, айнымалы-лардың мәндері бойынша бүтін санды, бірақ оңтайлы емес. Өйткені мақсат функцияның мәнін әлі де болса жоғарылататындай бүтін-сандылық шешім бар. Ондай шешімді 5-ші есептен алдық және ол шешім оңтайлы.
Айнымалылар мәндері бүтін санды болу шарты қарастырыл-маған, «Бұтақ және шекара» әдісінің алгоритмі бойынша, 1-ші бөлімде келтірілген тәсілмен, жоғарыдағы қарастырылған әрбір есептің сызықтық модельдерінің MS Excel көмегімен алынған шешімдерді MS Excel-де сценарияға жазайық. Мысалға, 1-ші есептің шешімі алынғаннан кейін Сервис → Сценарии.. бұйрығын іске қосамыз. Диспетчер сценариев сұхбаттасу терезесі ашылады. Добавить батырмасын шертеміз. Название сценария терезесіне сценария атын жазамыз: 1-есеп (2.1-сурет).
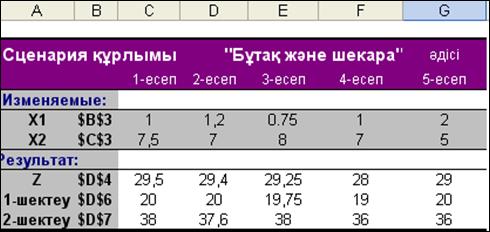
2.1-сурет. «Бұтақ және шекара» әдісі алгоритмі бойынша бір есептің оңтайлы шешімін табу барысында шығарылған есептер
Әрі қарай келесі кезектегі есептің шарттары бойынша кестелік модельге түзетулер енгізіп, Поиск решенияқұралымен шешімдерді алғаннан кейін, оларды сценарияға жазу әрекеттері қайталанады. Осылай құрылған, барлық есептердің шешім нәтиже-лері, яғни сценария құрлымы 2.1-суретте келтірілген. Суреттен көріп отырмыз, сценария құрлымы толығымен қолмен құрылған 2.1-кестедегі мәліметтерді қайталады. Осы процедуралардан кейін алғашқы 1-есеп, айнымалылардың бүтінсан болу шарты (ол тура-лы келесі есепте түсініктеме беріледі) бойынша, MS Excel-де Поиск решенияқұралында қарастырылған «Бұтақ және шекара» әдісімен қайта шығарылды. Есептің шешім нәтижесі 2.2-суретте келтірілген. Онда жоғарыда жеке-жеке шешілген әрбір есептер «автоматты» түрде бірге қарастырылып, есеп бірден шешілді, яғни ешқандай қиындықсыз оңтайлы шешімді алдық.

2.2-сурет. «Бұтақ және шекара» әдісімен бірден анықталған оңтайлы шешім
Сонымен берілген есепті шешу нәтижесінен “Бұтақ және шекара” әдісі бүтін санды оңтайлы шешімді қамтамасыз ететініне және осы әдіс компьютерде жеңіл орындалынатынына көз жеткіздік. Ең бастысы, осы әдісті тәжірибеде қолдану нәтижесінде, бөлшек мәнді шешімге жай қарапайым «дөңгелектеу» ережесін қолдану, бүтінсанды оңтайлы шешім алуды қамтамасыздандыра алмайды деп қортынды жасалынды.
Дата добавления: 2015-11-18; просмотров: 2950;

