Бульдік айнымалылармен есептер
Бульдік айнымалылар есебі, ізделінетін айнымалылар xj кез келген бүтін мәнді емес, тек мына екеуінің: 0 немесе 1, біреуін қабылдайтын, бүтін санды айнымалы есептерінің жекеленген түрілеріне жататын есеп. Мұндай айнымалыларды, бүтін санды-лардан ажырату үшін, xj орнына δj мен белгілейміз. Осындай айнымалыларды бірінші рет ұсынған ағылшын математигі Джордж Бульдің құрметіне, оларды бульдік айнымалылар деп атаған. Кейде оларды екілік айнымалылар деп те атайды.
Халық шаруашылығында, оның ішінде ауыл шаруашылы-ғында бульдік айнымалы есептер жиі кездеседі. Мысалға, тәжірибе-де бір мәселені бірнеше нұсқада шешуге болады, ал олардың қайсысы тиімді? Сөзсіз, тиімді нұсқаны шешімдер ішінен таңдау қажет. Осындай бір қарапайым есепті шешу арқылы, бульдік айны-малыларды қолдану тәсілдерін қарастырайық.
Есеп.Шаруа қожалығында бар қорларды 4 нұсқада қолдануға болады. Бірақ, әрбір нұсқада әртүрлі шамада пайда алынады және қорларда әртүрлі мөлшерде қолданылады. Максимальды пайда да қорлар тиімді қолданылмауы немесе аз пайдамен қорлар шығынын азайтып, оларды басқа мақсатқа қолдану тиімді болуы мүмкін. Сонымен, “қорларды қандай нұсқада қолданған тиімді?” деген сұраққа жауап табу керек.
Жалпы есепті шығаруға керекті мәліметтерді 2.4-кестеден алуға болады.
2.4-кесте. Шаруа қожалығында қорларды қолдану нұсқалары
| Нұсқалар | Қорлар мөлшері | ||||
| Пайда | – | ||||
| Еңбек | |||||
| Қаражат |
Осы кестеде келтірілген нұсқалардың қайсысы шаруашы-лыққа пайдалы немесе қандай нұсқаларды сәйкес қолданғанда пай-далар сомасы максимальды болатынын табу керек.
Мынадай шартты қабылдайық:
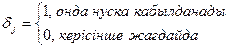
Олай болса есептің математикалық моделі мына түрде жазылады:
Z = 70δ1+ 80δ2 + 90δ3 +210δ4 → max
10 δ1+ 15 δ2 +22 δ3 +28 δ4 ≤ 50
200 δ1 + 1802 δ2 +240 δ3 + 250 δ4 ≤ 650
0≤ δj ≤ 1; i = 1,2, 3, 4
δj – бүтін сандар, i = 1,2, 3, 4
Бульдік айнымалы есептерді шешу. Есептің MS Excel жұмыс бетіне кестелік модель құрылады (2.9-сурет). Сервис …, Поск решения құралын қосып, сұхбаттасу терезесіне мақсат функция адресін F7 және бағытын Максимальное белгілейміз. Айнымалылар: B3:E3 ұясын енгіземіз.
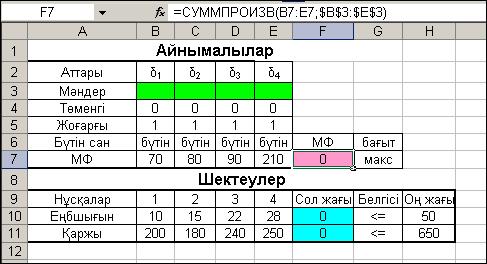
2.9-сурет
Шектеулер шарттарын енгізуді бастаймыз. Бульдік айныма-лылардың төменгі: B3:E3 ≥ B4:E4 және жоғарғы: B3:E3 ≤ B5:E5 шектеулерін және бүтін сан болу талабын: B3:E3 – целые. Пара-метры батырмасын басып, келесі сұхбаттасу терезесіне өтіп, одан Линейная модель жолын белгілеп, ОКжәне Выполнить батырма-ларын іске қосамыз. Есептің шешімі 2.10-суретте көрсетілген. Алынған нәтижеде: δ3=1, δ4 =1, сөйтіп, пайда Z = 300 максималь-ды болатын, 3 және 4 нұсқаларды қабылдау керек.
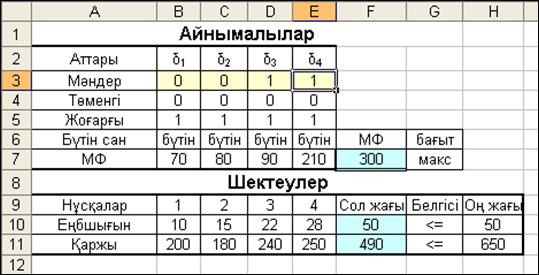
2.10-сурет
Бульдік айнымалы есептерде есептің нәтижесін талдау тәсілдерінің барлық түрін қолдануға болады. Солай болғанымен де, тек нәтижені талдаудан тұратын, бүтін сандылар есептері, оның ішінде бульдік айнымалылар есептері үшін оңтайлы шешімді талдау ешқандай да жаңалық емес. Демек, бульдік айнымалы есеп-терінің әртүрлі шектеулерінде, оңтайлы шешімдерін іздегенде, нұсқалық талдауға қарағанда тәжірибеде құрамдық талдау жасау қызықты. Сондықтан шешімнің 1-ші нұсқасын сақтаймыз. Ол үшін Сохранить сценарий... батырмасын басып, осы сақталған нәтиже-нің атын, яғни «1-нұсқа» депенгіземіз де, «ОК» және «ОК» батырмасын басамыз.
Бульдік айнымалыларды қолдану арқылы шығарылатын есептерге мынадай: «если...., то...» және т.б. көптеген логикалық шарттарды қоюға болады. Осындай шарттардың кейбіреуін қарас-тырайық.
Егер оңтайлы шешімге міндетті түрде (ДОЛЖЕН) бір нұсқа немесе (ИЛИ) басқа нұсқа, онда осы шарт мына түрде жазылады:
δi + δj =1.
Егер оңтайлы шешімге мүмкін (МОЖЕТ) бір нұсқа және (И) басқа (енеді немесе енбейді), онда осы шарт мына түрде жазылады:
δi + δj ≥ 0.
Мына жағдайда, егер оңтайлы шешімге i- нұсқа қабылдан-ғанда j- нұсқа міндетті түрде енетін болса, онда осы шарт мына түрде жазылады:
δi = δj немесе δi - δj = 0.
Сөйтіп, міндетті болған жағдайда теңдік белгісі «=», ал мүмкін болған жағдайда теңсіздік “≥” белгісі жазылады.
Демек, қабылданған k-нұсқада i немесе j нұсқалардың біреуінің қабылдануының шарты былай жазылады:
δi + δj = δk немесе δi + δj - δk = 0.
Осыларға сәйкес үш нұсқалар үшін де логикалық шарттар жазуға болады. Сөзсіз, мұндай логикалық шарттар шектеусіз. Сонымен логикалық шарттарды жазу тәртіптерімен танысқаннан кейін бульдік айнымалы есептерді құрамдық талдауға көшеміз.
Айталық, жоғарыда қарастырылған есепте:
а) егер 4-нұсқа қабылданса, онда 2-нұсқада қабылданатын болсын, яғни δ2 = δ4 немесе δ2 - δ4 = 0;
б) барлық нұсқалар ішінен кем дегенде 3 нұсқа бірдей қабылдануға тиіс делік, онда: δ1 + δ2 + δ3 + δ4 ≥ 3.
Енді осы қойылған шарттарды есептің MS Excel-дің жұмыс бетіне кестелік моделіне енгізіп, оны шешу жағын ойластырайық (2.11-суретті қараңыз).
Бірінші кезекте есепті а) шартымен шешеміз. Сервис. Поиск решения... Добавить...F12=H12, мұндағы F12 ұясында, яғни қосымша шектеудің сол жағы: =СУММПРОИЗВ(B12:E12; $B$3:$E$3) формуласы жазылған. «ОК», Выполнитьжәне Сохранить сценарий... батырмасын басып, осы сақталған нәтиженің атын «2-нұсқа» депенгіземіз де, «ОК» және тағы да «ОК» батырмасын басамыз.
Екінші кезекте б) шартты бойынша есепті шешеміз. Жоғарыдағы іс-әрекеттер сол реттерімен тағы да қайталанылады. Тек, F12 = H12 шарты шектеулер жүйесінен алып тасталынады. Оның орнына, Добавить...көмегіменF13 >=H13, мұндағы F13 ұясында, яғни қосымша шектеудің сол жағы: =СУММПРОИЗВ-(B13:E13;$B$3:$E$3) формуласы жазылған. Нәтиженің атын «3-нұсқа» депенгіземіз де, сақтаймыз. Осымен есепті, шектеулердің 3-нұсқасында шығару жұмысы аяқталды.
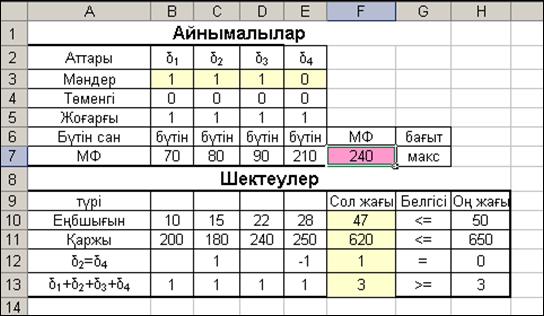
2.11-сурет
Сценарияларда жинақталған есепті алуға кірісеміз. Мынадай әрекеттер арқылы: Сервис, Сценарии.., Отчет(есеп)...СтруктуражәнеОК,құрамдық талдау нәтижелерін алдық.Экранда: Сценария құрамы. Көзге көрнектілеу үшін біраз түзетулер енгіземіз. Түзету-лерден кейін сценария құрамы 2.12-суретте көрсетілген.
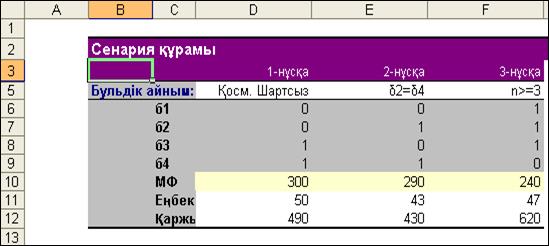
2.12-сурет
Осы деректер бойынша диаграмма тұрғызылды (2.13-сурет).
Диаграммадан қосымша енгізілген логикалық шарттар мақ-сат функцияға қалай әсер ететінін байқауға болады. Сонымен, кезкелген қосымша шектеулер сияқты, логикалық шарттар мақсат функция мәнін жақсартпай, төмендетеді деп қортындылаймыз.
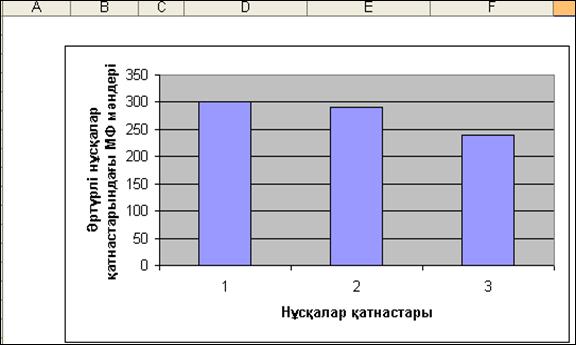
2.13-сурет
Дата добавления: 2015-11-18; просмотров: 2186;
