Бүтін санды модельдер

Тарихи деректер бойынша бүтін санды теңдеулерді шешумен ғалымдар ертеден айналысқан. Мысалға, Гректік математик Диофант (II–III ғ.ғ.) теңдеулердің шешімінде ізделініп отырған белгісіз тек бүтін мәнді болады деп қарастырған. Бүгінгі әдебиет-терде бүтінсанды модельдердің негізін 1932 жылы Венгер матема-тигі Е. Эгервари қалыптастырды делінеді. Ол әрбір ұшақтар жолы-на белгілі бір ұшақтарды бекітумен және әртүрлі жұмыстарға механиктерді бөлумен айналысқан.

Оңтайластыру модельдерін шешу нәтижесінде мәндері ізде-лініп отырған айнымалылар міндетті түрде бүтінсандар болуға тиіс болса, онда мұндай модельдерді бүтін санды программалау мо-дельдері деп атаған. Бүтін сандық шешім тек сызықтық програм-малау есебіне келтірілген кейбір есептерге ғана тән талап емес, шешімнің бүтін санды болуы кейде сызықты емес программалау есептерінде де кездеседі. Сондықтан, егер шектеулер және мақсат функциясы сызықты байланыста болса, онда мұндай есепті сызық-тық программалаудың бүтін санды есебі деп атайды; егер кемінде бір байланыс сызықты емес болса, онда мұндай есепті сызықты емес программалаудың бүтін санды есебі деп атайды.

Халық шаруашылығы есептерінің көбісінде бүтін санды бел-гісіздер кездеседі. Сөзсіз, мұндай сандар физикалық түрде бөлін-бейді, себебі, екі жарым жаңа кәсіпорнын ұйымдастыруға, бір жарым автокөлік сатыпалуға, қырық жарым мал бордақылауға, он жарым жұмыскерді жұмысқа қабылдауға және т.б. болмайды. Сөйтіп, сызықтық программалау есептеріне ұқсас көптеген халық шаруашылық есептеріне бүтін санды шешім қажет. Мысалға, мал табынының тиімді айналымы, ауылшаруашылық техникаларын әр түрлі жұмыстарға бекіту, өндіріс орындарының өндіретін бұйым-дарының тиімді санын анықтау және т.б.с.с.

Бүтін санды программалау есебінің пайда болуын Данциг-тың, Фулкерсонның және Джонсонның “Кесіп тастау” әдісінің идеясымен байланыстырады. Бірақ бүтін санды программалау есебінің бүгінгі дамуы, кесіп тастау идеясын іс жүзіне асыру үшін жасалған Гомори ұсынған бірінші алгоритм пайда болуынан кейін басталды. Бұл әдіс кейіннен Гоморидің атымен, Гомори әдісі деп аталынды. Сонымен, бүтін санды модельдерді шешу әдістерін күрделенген оңтайластыру әдістерінің қатарына жатқызуға болады.

Бүтін санды модельдерді шешу әдістерінің ерекшеліктеріне тоқталайық.

Бүтін санды модельдер сыныбына, айнымалылары теріс емес тек бүтін мәндер қабылдайтын, мақсат функция өзінің аргумент-терімен сызықты байланыста болатын және шектеулерінің сол жағы сызықты теңсіздік немесе теңдік түрінде берілген, бір крите-риялды оңтайластыру есептері жатады. Сонымен қатар айнымалы-лар шамаларына, келесі тақырыптарда қарастырылатын бульдік айнымалыларға қойылатын шектеулер сияқты, қосымша шектеулер қойылмайды Бүтін санды сызықты программалау есебінің жалпы математикалық қойылуын қарастырсақ, осы сынып есептері туралы нақтылы анықтама түсінікті бола бастайды. Демек, жоғарыда кел-тірген анықтама негізінде бүтінсанды сызықты программалау есебінің математикалық моделін мына түрде өрнектеуге болады:

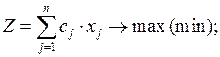
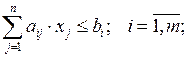(2.1)

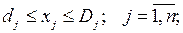
x_j ≥ 0, j = 1,...n, x_j – бүтін сандар, j = 1,..k.

Келтірілген (2.1) жүйенің байланыстарына қарасақ, оның сызықты программалау және оған ұқсас есептерден ешқандайда айырмашылығы жоқ екенін байқаймыз. Дегенмен де, жалғызғана айырмашылық бар. Ол есептің шешімін күрделіндіретін және оған үлкен әсер ететін, мына: x_j – бүтін сандар, j = 1,..k шарты. Бүтін сандар саны k төменгі екі нұсқаның біреуін қанағаттандыруға тиіс.

Егер k = n, мұндағы n – айнымалылардың жалпы саны, онда барлық айнымалылар мәні тек бүтін сан болуға тиіс; мұндай жағдайда есеп толық бүтін санды деп аталады. Егер k < n, яғни тек k дейінгі айнымалылар бүтін санды, ал қалғандары өздерінің шеткі шекаралықтарына дейін кез келген мән қабылдай алатын болса, онда мұндай есептерді жарым-жартылай бүтін санды деп атайды. Осы жерде, толық бүтін санды есептерді шешу үшін барлық бүтін санды айнымалылар жоғары жағынан міндетті түрде шектеулі болу керектігін атап өтейік.