Бүтін санды модельдерді MS Excel көмегімен
Шешу алгоритмі
Шартты үздіксіз сызықты модельдерден құралатын есептер симплекс әдісімен, симплекс кестелерін құру арқылы шешілетіні және осы әдістің алгоритмі көптеген пакеттерде компьютер тіліне өткізіліп, программалар құрылғаны белгілі. Осы әдістің, «Әрекет-терді зерттеу» [1], «Математикалық программалау» [16], «Эконо-микалық-математикалық әдістер» [15] және «Менеджментте мате-матикалық әдістер» [12] пәндерінде баяндалған теориясынан, әрбір қадамда кезекті жақсартылған симплекс кесте құрылатыны және осы кесте бойынша нақтылы қарастырылатын белгілер негізінде мынадай сұрақтарға: есепте мүмкін бола алатындай шешім барма және алынған кестедегі мәндер есептің шешімі бола ала ма? және ол оңтайлы ма?, жауап алынатыны айтылған. Есептің шешімі бар болса, онда аталған сұақтарға жауап беретін белгі (ереже бойынша қарастырылатын белгілердің біреу орындалса, онда алынған шешім мүмкін бола алатыны, ал егер екеуі де орындалса шешім оңтайлы делінеді) табылғанша қайта-қайта жаңа сиплекс кестесі тұрғызыла береді. Бүтін санды есептерді шешкенде мұндай белгілер қарастырылмайды, сондықтан кезекті алынған нәтиже бойынша есептің мүмкін бола алатын шешімі алынғанына және шешімнің оңтайлығына жауап алынбайды. Міне осындай қиындықтарға қарамастан, бүтін санды модельді «Бұтақ және шекара» әдісі бойынша шешу қарастырылған MS Excel құралы оңтайлы шешімді нақтылы дұрыс анықтайды.
Бүтін санды модельдерді MS Excel көмегімен шешу бары-сында жасалынатын жұмыстардың реті 1-ші бөлімде баяндалған сызықты модельдерді шешу технологиясымен бірдей. Сонымен қатар есепті шығару барысында, айнымалылар үздіксіз және бүтін санды болған жағдайда олардың нәтижелерінің дәлдігін бағалау үшін есептің шешімдерін салыстыруға болады.
Бүтін санды модельді MS Excel көмегімен шешу технология-сының кейбір ерекшеліктерін мынадай мысал арқылы қарасты-райық.
Төрт түрлі бұйымдарды: A, B, C және D даярлауға үш түрлі қор: еңбек, шикі зат және қаржы қажет, оларды қанша данадан шығару керектігін анықтайық. Бұйымдардың бір данасына есептелінген қорлардың шығындары және бір дана бұйымдардан түсетін пайда 2.2-кестеде берілген.
2.2-кесте. Есептің алғашқы деректері
| Қорлар | Бұйымдар | Қорлар мөлшері | |||
| A (X1) | B (X2) | C (X3) | D (X4) | ||
| Еңбек | |||||
| Шикізат | |||||
| Қаржы | |||||
| Пайда | – |
Математикалық модель құрамыз, ол үшін мынадай белгілерді қабылдаймыз:
xj – өндірілетін j – түрлі өнімнің оңтайлы саны, 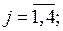
bi – i – ші қордың шаруашылықта бар мөлшері, 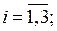
aij – i – ші қордың j –шы өнімнің бір данасын өндіруге керекті мөлшері;
cj – j – шы өнімнің бір данасынан алынатын пайда.
Осыдан есептің математикалық моделі мына түрде жазылады:
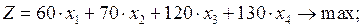
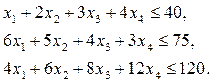 (2.2)
(2.2)
xj ≥ 0, j = 1,2,3,4 xj – бүтін сандар, j = 1,..4.
MS Excel –дің жұмыс бетіне кестелік модельді құрамыз. Ол үшін мынадай іс-әрекеттер жүргізіледі:
1. Кестелік модельге керекті комментарияларды арнайы ұяларға (2.3-сурет) енгіземіз. Бұл ұялардағы жазулар қарастырылып отырған есептің шешіміне ешқандай да әсер жасамайтынын тағы да ескерте кетейік.
2. B6:E6аралықтағы ұяларғамақсат функция коэффициент-терін енгіземіз: с1 = 60, с2 = 70, с3 = 120, с4 = 130.
3. F6ұяға мақсат функция формуласын енгіземіз: =СУММПРОИЗВ(B4:E4; B6:E6).
4. B9:E11 аралықтағы ұяларға шектеулердің коэффициент-терін енгіземіз.
5. H9:H11 аралықтағы ұяларға шектеулердің оң жағын: b1 = = 40, b2 = 75, b3 = 120 енгіземіз.
6. F9ұяға бірінші шектеудің сол жағының формуласын жазамыз: =СУММПРОИЗВ($B$4:$E$4;B9:E9).
7. F9ұядағы формуланы F10жәнеF11ұяларға белгілі әдіспенкөшіреміз.
8.I9ұясынашектеудің оң жақ бөлігімен сол жағының айырмашылығынбілдіретінформуланы: =I9 – F9 жазамыз.
9.I9ұядағы формуланы,в ячейки I10және I11ұяларға көшіреміз.
Сонымен Excel-дің жұмыс бетінде қарастырылып отырған есептің кестелік моделінің сыртқы пішіні 2.3-суретте көрсетілген.
Есепті әрі қарай шешу үшін Поиск решения шақырылады. Ол үшін бас менюдан: Сервис Þ Поиск решения...
Сұхбаттасу терезесінде Поиск решенияпайда болғаннан кейін төменгідей іс-әрекеттер орындалынады:
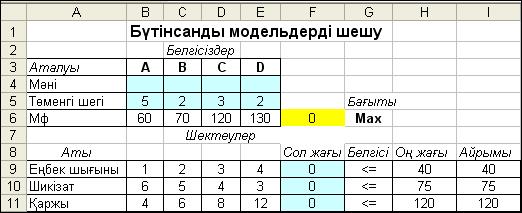
2.3-сурет. Бүтін санды есептің кестелік моделі
1. Установить целевую ячейкужолына мақсаттық ұяның абсолюттік $F$6адресін көрсетеміз, яғни курсорды мақсат функция формуласы жазылған ұяға орналастырамыз.
2. Равной:тобы үшін, максимальному значению –нұсқасын іздеуді таңдаймыз.
3. Изменяя ячейкижолынамәндері ізделінетін айнымалы-лардың абсолюдтік $B$4:$E$4адрестерін енгіземіз.
4. Келесі кезекте шектеулерді, айнымалылардың төменгі және жоғарғы шектерін, теріс болмау және бүтін санды болу шарттарын енгіземіз. Осы мақсаттарға жету үшін келесідей іс-әрекеттер орындалынады:
· шектеулерді енгізу үшін Поиск решения-ныңалғашқы сұхбаттасу терезесіндегі Добавить батырмасын басамыз (2.4-сурет);
· қосымша пайда болған сұхбаттасу терезеде Ссылка на ячейку: жазуының астындағы терезеге $F$9:$F$11ұялар аралығыбейнеленеді;
· шектеулердің жиналып тұрған белгілері тізімдерінің ішінен кестелік модельде көрсетілген белгіні “<=” таңдаймыз;
· Ограничение: жазуының астындағы терезеге $H$9:$H$11аралықтарында тұрғанұялардағы шектеулердің оң жақтары енгізіледі;
· шектеулерге қосымша шарттарды енгізу үшін осы қо-сымша сұхбаттасу терезесіндегі Добавить батырмасын іске қосамыз (2.5-сурет).
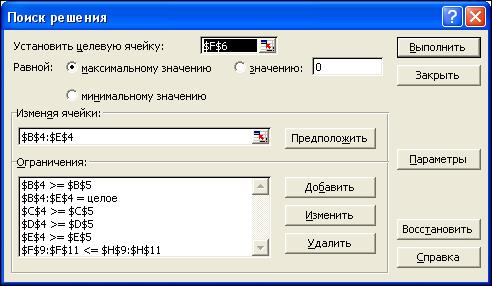
2.4-сурет. Поиск решения –ның сұхбаттасу терезесі (барлық
шектеулер енгізілгеннен кейінгі бейне)
5. Шектеулер қатарына, айнымалылардың мәндері олардан кем болуы мүмкін еместігін білдіретін төменгі шекара шектеулерін және бүтін сан болу шарттарын енгіземіз. Осы мақсат үшін келесі іс-әрекеттер орындалынады:
· қосымша сұхбаттасу Добавление ограничения терезесіне айнымалыларың төменгі шекара шектеулерін екі нұсқада енгізуге болады: біріншісінде,Ссылка на ячейку жазуы астындағы терезеге бірден ұялардың адрес аралығын, мысалға, біздің жағдайда $B$4:$E$4 немесе екінші нұсқада, әрбір айнымалыны жеке-жеке B4, C4, D4, E4 енгіземіз;
· түсіп кеткен, көрінбей тұрған белгілер тізімінен кем емес “≥” белгісін таңдаймыз;
· айнымалылардың төменгі шекара шектеулерінің мәндері тұрған, бірінші нұсқада Ограничение жазуы астындағы терезеге бірден ұялардың адрес аралығын, біздің мысалда $B$5:$E$5 немесе екіншісінде, әрбір мәндерді жеке-жеке B5, C5, D5, E5 енгіземіз;
· қосымша сұхбаттасу Добавление ограничения терезе-сіндегіСсылка на ячейку жазуы астындағы терезеге айнымалылар мәндері алынатын ұялар аралығын $B$4:$E$4жазамыз;
·түсіп кеткен, көрінбей тұрған белгілер тізімінен, бүтін сан шартын білдіретін “цел” жазуын таңдаймыз;
·шектеулердіңоң жақтарының мәндері тұрған ұялардың адрестерін көрсетуге арналған Ограничение жазуы астындағы терезені сол қалпында қалдырамыз, онда Поиск решения «автоматты» түрде «целое» деп жазады (2.5-сурет);
· соңғы шектеуді енгізу үшін ОК батырмасын басамыз.
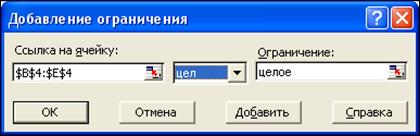
2.5-сурет.Добавление ограничения-қосымша сұхбаттасу терезесі
(соңғы әрекет кезеңі)
6. Поиск решения → Параметрлер арқылы қосымша сұхбаттасу терезесінен Линейная модель, Неотрицательные значенияжәне Автоматическое масштабирование жазуларын белгілейміз (2.6-сурет).
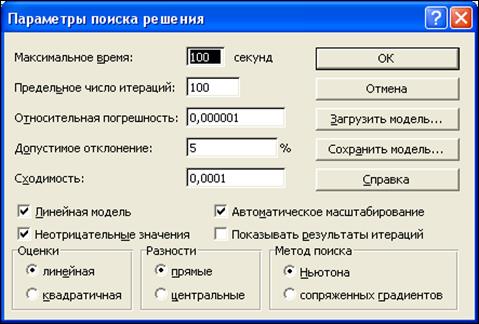
2.6-сурет. Поиск решения параметрлері
7. Жоғарыдағы әрекеттерді тиянақты орындағаннан кейін есепті шешуге көшеміз. Ол үшін Выполнить батырмасын іске қосамыз. Оңтайластыру үрдісі орындалғаннан кейін сұхбаттасу терезесі Результаты поиска решенияашылады (2.7-сурет).
2.7-сурет.
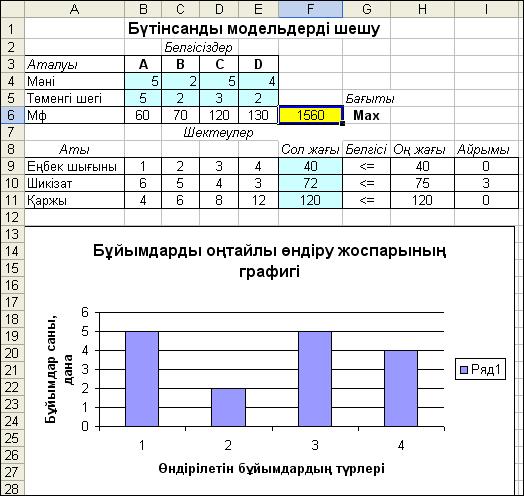
2.8-сурет. Есептің оңтайлы шешімінің нәтижелері
8. Сохранить найденное решение жазуынбелгілейміз де,ОКбатырмасын шертеміз.Программа MS Excel – де есептеуді аяқтағаннан кейін, есептің 2.8-суретте көрсетілген нәтижесін сандық және графикалық түрде аламыз.
Есептің шешім нәтижесінде ізделініп отырған айнымалы-лардың оңтайлы мәндері анықталынды: х1 = 5; х2 = 2; х3 = 5; х4 = 4 , оларға мақсат функция мәне z =1560 а.б. сәйкес келеді.
Есептің шешімін талдау нәтижесінде, егер бұйымдар мынадай қатынаста: А→ 5 дана, В→ 2 дана, С→ 5 дана және D→4 дана өндірілетін болса, онда максимальды пайда табу қамтамасыз етілетіні анықталды. Сонымен қатар, шаруашылықтағы еңбек және қаржы қорлары түгелдей қолданылатыны және 3 ө.б. шикізат қоры қолданылмай қалатыны белгілі болды. Сөйтіп, шаруашылықта шикізат қоры 3 ө.б. артық мөлшерде екені, оны басқа мақсат үшін немесе сыртқа сатуға болатындығы жөнінде шешім қабылданды.
Бүтін сандық және үздіксіз шешімдер нәтижелерін салысты-ру үшін, айнымалылардың бүтін санды болу шартын алып тастап, қарастырылып отырған есеп, Поиск решения құралымен қайта шығарылды. Шешім нәтижелері бойынша 2.3-кестені тұрғыздық.
2.3-кесте
| Шешімдер | Х1 | Х2 | Х3 | Х4 | МФ | S1 | S2 | S3 | |
| Үздіксіз | 6,71 | 2,71 | 1598,57 | 1,71 | |||||
| Бүтінсанды |
Ескерту: S1, S2 және S3 белгілері, сәйкесінше еңбек, шикізат және қаржы қорларының қолданбай қалған мөлшерлерін көрсетеді.
Кестеден мыналар туындалды:
îүздіксіз шешімдеөндірілетін С(х3) және D(х4) бұйымдар-дың мәндері көп өзгеріске ұшырады. Біріншіден, олар бөлшек сандар, екіншіден, алынған бөлшек сандарды жай қарапайым «дөңгелектеу» арқылы бүтін сандарға айналдырсақ: х3=6,71≈7 және х4=2,71≈3 жүйедегі шектеулер шарттары бұзылады (42>40, 77>75 және 124>120). Сөйтіп, бүтін сандық шешім алу үшін жай қарапайым «дөңгелектеу» тәсілін қолдануға мүлдем болмайды;
îүздіксіз және бүтін сандық шешімдерде мақсат функция бір-біріне өте жақын. Дегенмен де, басқа да шарттар сияқты бүтін сандық шарт мақсат функция мәнін төмендетеді (1598,57– 1560 = =38,57);
îүздіксіз шешімде қаржы қоры 1,71 ө.б. қолданбай қалатыны анықталса, ал бүтін сандық шешімде керісінше шикізат қоры 3 ө.б. артық. Демек, есептің алғашқы мәліметтері бірдей болғанымен, айнымалылардың бүтін санды болу шарты, оның нәтижесін айтарлықтай өзгеріске әкелетініне көз жеткіземіз.
Дата добавления: 2015-11-18; просмотров: 2504;
