СИСТЕМА ЗАЛИШКОВИХ КЛАСІВ

Результати досліджень, що проводились різними групами вчених з метою пошуків шляхів підвищення продуктивності обчислювальних засобів, методів організації ефективної системи виявлення та виправлення помилок, а також побудови надійних обчислювальних комплексів, дають можливість стверджувати, що в межах позиційних систем числення не можна очікувати принципових зрушень в даних напрямках без суттєвого збільшення робочих частот і ускладнення апаратної частини. Причина полягає в тому, що позиційні системи числення, в яких представляється і обробляється інформація в сучасних ЕОМ, мають важливий недолік – наявність міжрозрядних зв’язків. Таким чином ефективним є використання непозиційних систем числення, які позбавлені даного недоліку.

З огляду на сучасний рівень розвитку обчислювальних засобів використання непозиційних систем числення дозволяє збільшити надійність та швидкість цифрової обробки даних, ввести методи контролю за правильністю виконання операцій без подальшого ускладнення апаратної частини та забезпечувати необхідну точність обчислень без збільшення розрядності шини. Сучасні обчислювальні потужності дозволяють розв’язувати задачі оптимального вибору модулів системи та розрахунку відповідних вагових коефіцієнтів та базисних чисел, що відкриває нові можливості застосування непозиційних систем числення.

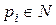Нехай задано набір із взаємопростих натуральних чисел , , тоді під СЗК будемо розуміти таку систему, в якій ціле число представляється у вигляді невід’ємних залишків по вибраних модулях .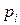

, . (1)

Даний вираз відповідає системі діофантових рівнянь:

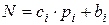, , (2)

де N – вихідна величина; 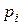– набір модулів; 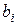– набір залишків по відповідних модулях; 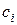– ранг числа N по модулю .

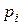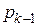
В теорії чисел доведено, що система рівнянь (2) має єдиний розв’язок при взаємопростих модулях. Діапазон чисел, що може бути представлений за допомогою набору модулів ( , , …, 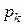) становить , .

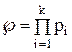Нехай у десятковій системі числення задано число N=13, вибираємо взаємно прості модулі: 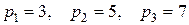, добуток яких .

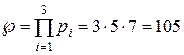Враховуючи, що 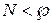можна використовувати даний набір модулів для перетворення заданого числа.

Спосіб 1.

При невеликому діапазоні представлених даних найбільш ефективним є табличний метод кодування та перетворення даних в СЗК .

Таблиця 2.1 – Таблиця кодування даних в СЗК.

Число в десятковій системі числення
…	…	….	….
…	…	….	….

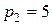
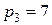
Отже, згідно таблиці 2.1: .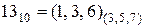

Спосіб 2. Нехай у десятковій системі числення задано число N=103.

Використовуючи рівняння (1) маємо:

;

;

.

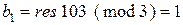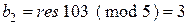Отже .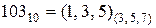

Спосіб 3. Задано число N=103.

Число N представлено в позиційній системі числення з основою 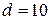. Представлення степенів основи d в СЗК буде мати вигляд:

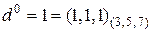б

,

.

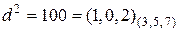Отримаємо представлення коефіцієнтів полінома (2.4).

,

,

.

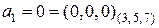Згідно формули (5):

.

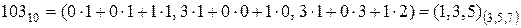Представлення числа N=103₁₀ отримані за допомогою різних методів аналогічні, що підтверджує достовірність отриманих результатів.

Переведення числа з системи залишкових класів в десяткову систему числення

Переведення числа з системи залишкових класів в десяткову систему числення здійснюється за формулою

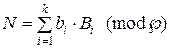. (3)

Згідно визначення ортогональних базисів, вони можуть бути обчислені:

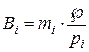, ; (4)

де 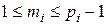– вага ортогонального елементу.

При чому

. (5)

Рівняння (5) еквівалентне наступному діафантовому рівнянню:

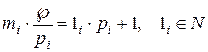. (6)

Для обчислення використовується формула (5). Застосування операції визначення залишку по заданому модулю обумовлює обмежений діапазон можливих значень вагових коефіцієнтів: .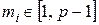

Позначимо 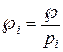. В результаті ділення на отримаємо певний залишок , згідно рівняння (5):

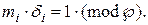(7)

З огляду на порівняно невеликі значення величини можемо скласти таблицю розв’язків рівняння (7), за допомогою якої згідно величини знаходиться відповідне значення . Припускаючи, що основи вибираються з множини простих чисел, приведемо таблицю розв’язків рівняння (7), для (таблиця 2.2).

Згідно (5):

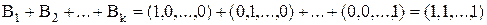. (8)

Оскільки сумування проводиться в СЗК:

. (9)

Таблиця 2.2 – Розв’язки рівняння 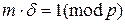для множини простих чисел

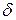
	Р
						4г

Рівняння (9) можна використати для перевірки достовірності знаходження базисів системи.

Розглянемо приклад зворотного перетворення для значень отриманих вище

.

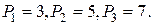
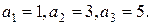
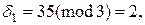
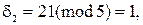
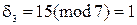Використовуючи означення базисних чисел та таблицю 2.2:

; ; ;

; ; .

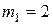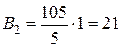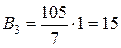Перевіримо достовірність обчислення базисних чисел згідно формули (9):

.

Згідно формули (3):

В результаті послідовного застосування прямого та зворотного перетворень для цілочисельної форми СЗК отримаємо вихідне число в позиційній системі числення.

Представлення даних в системі залишкових класів дає змогу здійснювати розпаралелювання обробки інформації без значного ускладнення обчислювальних засобів. Використання СЗК спрощує побудову систем збору інформації, а також дозволяє вирішувати клас задач, що є невизначеними в позиційних системах числення. Особливістю СЗК залишається простота реалізації прямого та зворотного перетворень.