ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ ЛОГІКИ
Перемикальні функції.
Булева алгебра одного, двох аргументів.
Закони алгебри логіки.
Теоретичною основою цифрових автоматів є алгебра логіки – наука, яка використовує математичні методи для розв’язування логічних задач. Алгебру логіки називають булевою на честь англійського математика Дж. Буля, який вніс великий вклад в розвиток цієї науки (1815-1864).
Основним предметом булевої алгебри є висловлювання – просте твердження, про яке можна стверджувати: істинне воно (позначається символом 1) або хибне (позначають символом 0).
Прості висловлювання позначають буквами, наприклад  , які у цифровій техніці називають змінними (аргументами).
, які у цифровій техніці називають змінними (аргументами).
За допомогою логічних зв’язок НЕ, АБО, І, ЯКЩО .. ТО будують складні висловлювання, які називають (логічними) функціями і позначають буквами F, L, K, M, P та ін.
У даний час головна задача алгебри логіки – аналіз, синтез і структурне моделювання будь-яких дискретних скінчених систем.
Змінну із скінченим числом значень (станів) називають перемикальною, а з двома значеннями – булевою.
Функція, яка має як і кожна її змінна скінченне число значень, називається перемикальною (логічною).
Логічна функція, число можливих значень якої і кожної її незалежної змінної дорівнює двом є булевою. Таким чином, булева функція – це окремий випадок перемикальної.
Операція – це чітко визначена дія над одним або декількома операндами, яка створює новий об’єкт (результат).
У булевій операції операнди і результат набувають “булевого значення 1” і “булевого значення 0”.
Булеву операцію над одним операндом називають одномісною, над двома – двомісною і т.д.
Булеві функції можуть залежати від однієї, двох і в цілому від n- змінних.
Запис  означає, що деяка булева функція F залежить від змінних
означає, що деяка булева функція F залежить від змінних 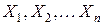 .
.
Основними булевими операціями є заперечення (операція НЕ, інверсія), диз’юнкція (операція АБО, логічне додавання, об’єднання) і кон’юнкція (операція І, логічне множення).
Заперечення – це одномісна булева операція 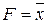 (читається “не Х”), результатом якої є значення, протилежне значенню операнда.
(читається “не Х”), результатом якої є значення, протилежне значенню операнда.
Диз’юнкція – це булева операція  (читається
(читається 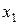 або
або  ) результатом якої є значення нуль тоді і тільки тоді , коли обидва операнди мають значення нуль.
) результатом якої є значення нуль тоді і тільки тоді , коли обидва операнди мають значення нуль.
Кон’юнкція – це булева операція  (читається
(читається 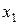 і
і  ) результатом якої є значення одиниці тоді і тільки тоді, коли значення кожного операнда дорівнює одиниці у виразі
) результатом якої є значення одиниці тоді і тільки тоді, коли значення кожного операнда дорівнює одиниці у виразі  .
.
Операції заперечення, диз’юнкції і кон’юнкції можна задати за допомогою таблиць істинності, у яких зліва подані значення операндів, а справа значення булевої функції.
|
|
Для булевих операцій заперечення, диз’юнкції і кон’юнкції справедливі такі закони, властивості й тотожності.
1) комутативність
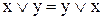
| 
|
2) асоціативність
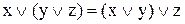
| 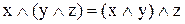
|
3) дистрибутивність

| 
|
4) ідемпотентність

| 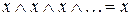
|
5) закон поглинання

| 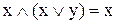
|
6) закон склеювання

| 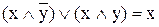
|
7) закон де Мограна
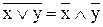
| 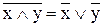
|
8) властивості заперечення і константи
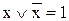
| 
| 
| 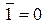 , , 
|
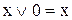
| 
| 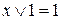
| 
|
Справедливість наведених законів булевої алгебри перевіряється підстановкою в логічний вираз нуля і одиниці, як показано в табл. 3.1. для різних логічних функцій.
Таблиця 3.1 – Таблиці істинності логічних функцій.
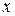
| 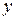
| 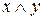
| 
| 
| 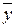
| 
|
Областю визначення булевої функції 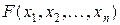 є скінчена множина різних двійкових наборів довжиною
є скінчена множина різних двійкових наборів довжиною 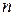 , на кожному з яких указується значення функції нуль або одиниця.
, на кожному з яких указується значення функції нуль або одиниця.
Кількість різноманітних двійкових наборів дорівнює множині 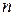 - розрядних двійкових чисел
- розрядних двійкових чисел  .
.
Наприклад для функції двох змінних 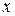 і
і 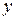 є чотири двійкових набори: 00; 01; 10; 11.
є чотири двійкових набори: 00; 01; 10; 11.
Дві функції відрізняються одна від одної, якщо їхні значення будуть різними хоч би на одному наборі.
Число різноманітних булевих функцій від 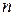 змінних дорівнює
змінних дорівнює 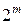 , де
, де  .
.
Довільну булеву функцію можна задати різними способами, часовими діаграмами, геометричними фігурами, графами, таблицями істинності та аналітичними виразами.
Словесний опис деякої булевої функції 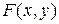 можна представити так:
можна представити так: 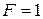 при
при 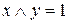 , і
, і  , якщо
, якщо  .
.
Таку функцію можна зобразити часовою діаграмою або геометрично за допомогою двовимірного куба у якому точками виділені одиничні вершини, а також графом, де вершини відображають значення нуля і одиниці, а на орієнтованих дугах змінні вказують на умови переходів ( рис.3.1)
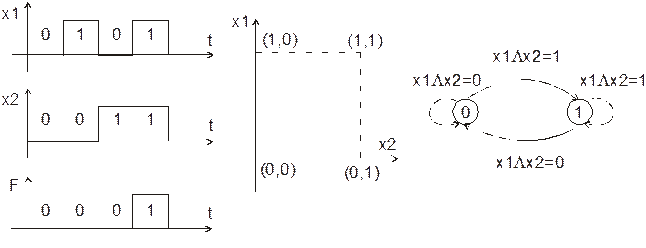
Рис. 3.1 – Способи зображення булевої функції
За допомогою таблиці істинності показують усі можливі функції однієї змінної (усього чотири функції) і двох змінних (усього 16 функцій).
Для 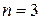 число можливих булевих функцій дорівнює 256, для
число можливих булевих функцій дорівнює 256, для 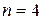 їхня кількість –
їхня кількість –  .
.
Булеві функції однієї змінної.
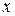
| Вираз | Назва функції | |
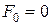
| Константа –0 | ||

| Повторення | ||

| Заперечення | ||
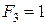
| Константа –1 |
Еквівалентність (рівнозначність) – двомісна булева операція, результатом якої є одиниця тоді і тільки тоді, коли операнди набувають однакових значень.
Імплікація (включення) – двомісна булева операція, результатом якої є значення нуль тоді і тільки тоді, коли значення одного з операндів дорівнює нулю, а іншого одиниці.
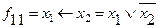 ;
;
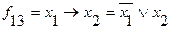 .
.
Виключення (заборона) – двомісна булева операція, результатом якої є значення одиниця тоді і тільки тоді, коли значення одного операнда дорівнює одиниці, а іншого – нулю.
 ;
;
 .
.
Булеві функції двох змінних (табл.3.1)
Таблиця 3.2 – Структурні формули та назви логічних функцій
| Аргументи | Функція | Назва логічної функції | |||
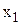 0 0
 0 0
| |||||
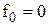
| Константа 0 | ||||

| Кон’юнкція, (операція І ) | ||||

| Заборона по 
| ||||
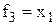
| Повторення (тавтологія) 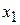
| ||||

| Заборона по 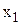
| ||||
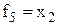
| Повторення (тавтологія) 
| ||||
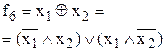
| Виключаючи АБО (додавання по модулю 2) | ||||
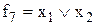
| Диз’юнкція (операція АБО); | ||||

| Стрілка Пірса (операція АБО-НЕ) | ||||

| Еквівалентність | ||||

| Заперечення (інверсія) 
| ||||
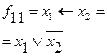
| Імплікація від  до до 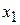
| ||||
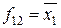
| Заперечення (інверсія 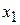 ) )
| ||||

| Імплікація від 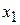 до до 
| ||||
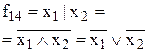
| Штрих Шеффера (операція І-НЕ) | ||||
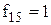
| Константа 1 |
Графічні позначення логічних елементів
| Назва операції | Назва елементу | Умовне графічне позначення | |
| Заперечення | НЕ | 
| 
|
| Диз’юнкція | АБО | 
| 
|
| Кон’юнкція | І | 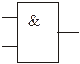
| 
|
| Заперечення диз’юнкції | АБО-НЕ | 
| 
|
| Заперечення кон’юнкції | І-НЕ | 
| 
|
| Еквівалентність | Виключаючи АБО | 
| 
|
| Заперечення еквівалентності | Еквівалентність | 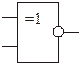
| 
|
| Імплікація | ЯКЩО, ТО | 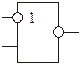
| 
|
| Заборона | ЗАБОРОНА | 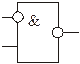
| 
|
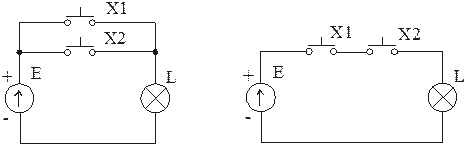
а) б)
Рис.3.2 – Схеми заміщення логічних елементів: а) логічний елемент АБО; б) логічний елемент І.
Контрольні запитання
1. Дайте визначення логічних функцій: інверсії, диз’юнкції, кон’юнкції.
2. Зобразіть умовні графічні позначення логічних елементів.
3. Запишіть таблиці істинності заданих логічних елементів.
4. Визначте вихідний стан логічних елементів при заданих вхідних сигналах.
5. Визначте якому логічному елементу належить таблиця істинності.
6. Які логічні елементи можна використати в якості інвертора ?
7. Запишіть закони алгебри логіки.
8. Спростіть логічний вираз:
8.1.  .
.
8.2.  .
.
8.3.  .
.
8.4. 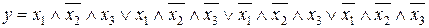 .
.
8.5. 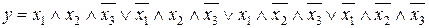 .
.
8.6. 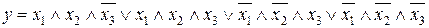 .
.
8.7. 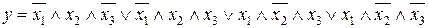 .
.
8.8.  .
.
Дата добавления: 2015-10-19; просмотров: 1971;
