СИНТЕЗ КОМБІНАЦІЙНИХ СХЕМ

Аналітичне представлення булевих функцій.

Етапи синтезу логічних схем на логічних елементах.

Розроблені універсальні (канонічні) форми представлення булевих функцій, які дають можливість одержати аналітичну форму довільної функції безпосередньо з таблиці істинності. Ця форма надалі може бути мінімізувати або спрощена.

Оскільки між множиною аналітичних представлень і множиною схем, які реалізують цю функцію, є взаємно однозначна відповідність, то пошук канонічної форми запису є початковим етапом синтезу логічних схем.

Найбільше поширення одержали досконала диз’юнктивна нормальна форма (ДДНФ) і досконала кон’юнктивна нормальна форма (ДКНФ). Для одержання цих форм вводяться поняття мінтермів (конституєнта 1) і макстермів (конституєнта 0).

Мінтерм – це функція 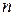змінних, яка дорівнює одиниці тільки на одному наборі.

Мінтерм одержують як кон’юнкцію 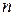змінних, що входять до нього у прямому виді, якщо значення даної змінної в наборі , і із запереченням, якщо . При 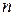змінних є 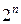мінтермів 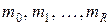, де .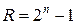

Всі мінтерми двох змінних наведені в таблиці 5.1.

Таблиця 5.1. Мінтерми двох змінних

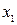
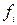
				Мінтерми	Макстерми

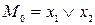
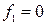
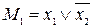
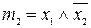
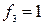
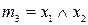
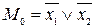
Значення функції , які відповідають, згідно з таблицею істинності, кожному і - му наборові, позначені через , , , .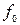

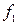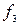Представлення функції у ДДНФ є диз’юнктивною сумою мінтермів, які відповідають наборам змінних, для яких .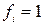

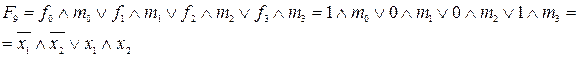
Макстерм – це функція 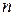змінних, яка дорівнює нулю тільки на одному наборі.

Макстерм одержують як диз’юнкцію усіх змінних, що входять до у прямому вигляді, коли значення , або в інвертованому вигляді, якщо значення .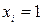

Число макстермів дорівнює 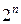, для функції двох змінних вони наведені в таблиці.

Представлення функції у ДКНФ записується у вигляді:

.

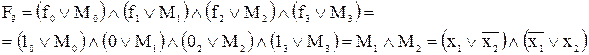Приклад. На прикладі табл.5.2 пояснимо аналітичний запис функції трьох змінних у ДДНФ і ДКНФ..

Таблиця 5.2. Таблиця істинності

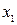
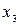
			Р

Для запису функції Р у ДДНФ потрібно диз’юнктивно скласти ті мінтерми, для яких функція дорівнює одиниці

.

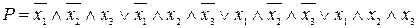Для запису функції Р у ДКНФ необхідно записати кон’юнкцію макстермів, для яких функція дорівнює нулю.

.

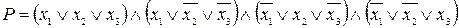За даним способом виконують запис у ДДНФ і ДКНФ функцій з довільним числом змінних.

Система функцій, суперпозицією яких може бути представлена будь-яка булева функція, називається функціонально повною і вона утворює базис у логічному просторі.

Систему функцій називають мінімально повним базисом, якщо видалення з неї будь-якої функції перетворює цю систему в неповну. В теорії алгебри логіки доведено, що функціонально повні системи утворюють такі набори функцій:

1. НЕ, АБО, І.

2. НЕ, АБО.

3. НЕ, І.

4. І-НЕ.

5. АБО-НЕ.

Інша алгебра логіки будується на основі функції суми за модулем два і кон’юнкції (алгебра Жегалкіна).

Через операції алгебри Жегалкіна можна виразити усі інші булеві функції.

Функціональну схему логічного пристрою одержують в результаті абстрактного синтезу, який складається з наступних етапів:

1) текстовий опис функцій логічного пристрою;

2) складання таблиці істинності за текстовим описом;

3) запис логічного рівняння пристрою у вигляді досконалої нормальної диз’юнктивної форми (ДДНФ) або досконалої нормальної кон’юнктивної форми (ДКНФ);

4) мінімізація логічного рівняння;

5) вибір одного із логічних базисів для реалізації функціональної схеми;

6) перетворення логічного рівняння з використанням правил де Моргана;

7) побудова функціональної схеми цифрового пристрою.

Приклад. Синтезувати логічний пристрій з трьома вхідними змінними, який генерує сигнал “1” на виході, якщо хоча би дві підряд змінні приймають значення “1”.

1. Складаємо таблицю істинності.

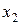
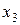
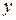
2. Логічне рівняння в виді ДДНФ представляє собою диз’юнкцію кон’юнкцій тих вхідних наборів, для яких :

.

3. Мінімізація логічного рівняння здійснюється шляхом використання законів алгебри логіки:

.

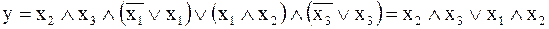4. Функціональну схему реалізуємо в базисі І-НЕ, для цього мінімізоване рівняння перетворимо по правилу де Моргана:

у базисі І-НЕ

,

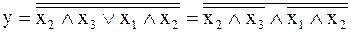в базисі АБО-НЕ

6. Функціональні схеми логічного пристрою реалізовані у базисах І-НЕ, АБО-НЕ представлені на рис. 5.1 і рис. 5.2.

Рис. 5.1 – Функціональна схема логічного пристрою у базисі І-НЕ.

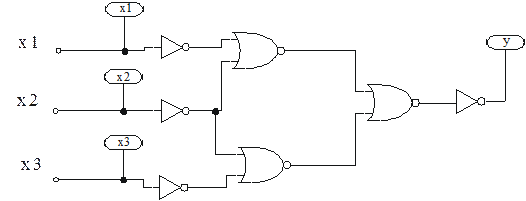
Рис. 5.2 – Функціональна схема логічного пристрою в базисі АБО-НЕ.

Контрольні запитання

1. Дайте визначення комбінаційного цифрового пристрою.

2. Назвіть етапи синтезу цифрових комбінаційних пристроїв.

3. Як записується досконала нормальна диз’юнктивна форма?

4. Як записується досконала нормальна кон’юнктивна форма?

5. Переведіть задане рівняння в базис І-НЕ, АБО-НЕ.

6. Синтезуйте функціональну схему пристрою за заданим рівнянням.