Способи переводу чисел з однієї системи числення в другу
Існують два основних способи переводу числа із однієї системи числення в другу: табличний і розрахунковий.
Табличний спосіб прямого переводу оснований на співставленні таблиць відповідності чисел різних систем числення. Цей спосіб дуже громіздкий і вимагає великого об’єму пам’яті для зберігання таблиці, але його можна використати для будь-яких систем числення (не тільки для позиційних).
Перевід цілих чисел із однієї позиційної системи числення в іншу
Нехай задано число А в довільній позиційній системі числення з основою 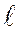 і його необхідно перевести в нову систему з основою Р.
і його необхідно перевести в нову систему з основою Р.
тобто 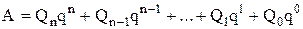 ,
,
 .
.
Необхідно перетворити до виду:
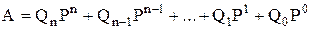 (1.1)
(1.1)
де  – база нової системи числення.
– база нової системи числення.
Вираз (1.1) можна записати:
 ,
,
де 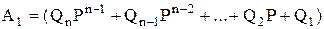 ,
,
 – залишок від ділення
– залишок від ділення  на
на  , який є цифрою молодшого розряду числа.
, який є цифрою молодшого розряду числа.
В результаті серії ділень вихідного числа на основу нової системи числення  знаходимо коефіцієнти:
знаходимо коефіцієнти:
 ;
;
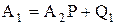 ;
;
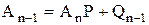 ;
;
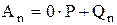 .
.
При цьому ділення продовжується до тих пір, поки не будуть виконуватися співвідношення:
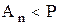 ;
; 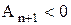 .
.
Правило переводу: щоб перевести ціле число із однієї позиційної системи числення в другу, необхідно задане число послідовно ділити на основу нової системи числення, записаної в числах старої (заданої) системи числення до одержання частки рівної 0.
Число в новій системі числення записується із залишків від ділення починаючи із останнього.
Приклади переводу.
Переведемо число 25 з десяткової системи числення в двійкову.
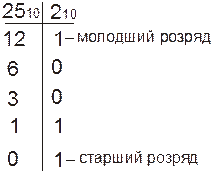
Отже  .
.
Переведемо число 92 з десяткової системи числення в вісімкову.
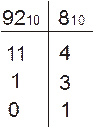
Отже 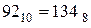 .
.
Переведемо число 168 з десяткової системи числення в шістнадцяткову.
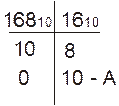
Отже  .
.
При переводі із двійкової системи числення в десяткову задане число необхідно ділити на основу нової системи числення тобто на  .
.
Оскільки ділення виконувати в двійковій системі трудно, тому на практиці підраховують суму степенів основи 2, при яких коефіцієнти 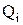 рівні одиниці.
рівні одиниці.
Розрахунки проводяться в десятковій системі числення.
Приклад.
1) Перевести двійкове число 10010100 в десяткову систему  :
:
 ;
;  .
.
2)  :
:
 ;
;
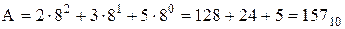 .
.
3) 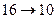 :
:
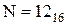 ;
;
 .
.
 ;
; 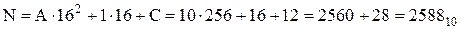 .
.
Перевід правильних дробів.
Щоб перевести правильний дріб із одної позиційної системи в другу, необхідно задане число послідовно множити на основу нової системи числення, записаної в старій системі числення до отримання заданої точності.
Дріб в новій системі числення запишеться в виді цілих частин добутку, починаючи з першої частини.
Приклад: Перевести правильний дріб 0,456 із десяткової системи числення в двійкову і вісімкову.
1) При переводі із десяткової системи в двійкову множимо заданий дріб на 2, а при переводі в вісімкову – на 8.
| Ціла частина | Дробова частина |
| х 8 8 8 |
| Ціла частина | Дробова частина |
Одержали: 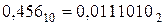 ;
;  .
.
2) При переводі із двійкової системи в десяткову множимо задане двійкове число на десять записане у двійковій системі числення (  ):
):

Одержані цілі частини переводимо у десяткову систему числення. Результат перетворення має вигляд:  .
.
Перевід неправильних дробів.
При переводі неправильних дробів необхідно окремо перевести цілу і дробову частини числа по вище розглянутих правилах переводу і записати в новій системі числення, залишивши без зміни положення коми.
Перевід чисел із системи числення в систему з кратною основою.
Якщо основи систем числення кратні одна одній, тобто зв’язані залежністю 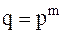 , то кожна цифра системи числення з основою
, то кожна цифра системи числення з основою 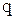 може бути представлена
може бути представлена 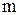 цифрами в системі з основою
цифрами в системі з основою  .
.
Відповідно, для того щоб перевести число із заданої системи числення в нову систему, основа якої кратна основі заданої системи, необхідно кожну цифру числа записати за допомогою 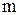 цифр в новій системі числення, якщо основа заданої системи більша за основу нової системи.
цифр в новій системі числення, якщо основа заданої системи більша за основу нової системи.
Наприклад, при переводі вісімкового числа  в двійкову систему числення достатньо кожну цифру вісімкового числа записати в виді двійкової тріади, так як
в двійкову систему числення достатньо кожну цифру вісімкового числа записати в виді двійкової тріади, так як  ,
, 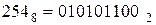 .
.
При переводі двійкового числа в шістнадцяткову систему достатньо кожну тетрaду заданого числа записати в виді шістнадцяткової цифри 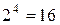 ,
, 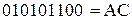 .
.
Вибір системи числення для використання в ЕОМ.
При виборі системи числення необхідно враховувати такі фактори:
1. Наявність фізичних елементів, здатних відтворити символи системи.
2. Економічність системи, тобто кількість елементів необхідних для представлення багаторозрядних чисел.
3. Трудоємність виконання операцій в ЕОМ.
4. Швидкодія обчислювальних систем.
5. Наявність формального математичного апарату для аналізу і синтезу обчислювальної системи.
6. Зручність роботи людини з машиною.
7. Завадостійкість кодування цифр на носіях інформації.
Дата добавления: 2015-10-19; просмотров: 3404;
