Позиційні системи числення.
1. Принципи побудови систем числення.
Числова інформація в комп’ютерах характеризується:
– системою числення (двійкова, десяткова та інші);
– видом числа (числа дійсні, комплексні, масиви);
– типом числа (змішане, ціле, дробове);
– формою представлення числа (місцем коми – з природною (змінною), фіксованою, плаваючою комами);
– розрядною сіткою і форматом числа;
– діапазоном і точністю подання чисел;
– способом кодування від’ємних чисел – прямим, оберненим та доповняльним кодами;
– алгоритмами виконання арифметичних операцій.
Системою числення називається сукупність цифр і правил для записування чисел.
Запис чисел у деякій системі числення називається його кодом.
Усі системи числення поділяють на позиційні й непозиційні. Для запису чисел у позиційній системі числення використовують певну кількість графічних знаків (цифр і букв), які відрізняються один від одного. Число таких знаків  називається основою позиційної системи числення.
називається основою позиційної системи числення.
В комп’ютерах використовують позиційні системи з різною основою.
Система числення з основою два (цифри 0 і 1) називається двійковою, система числення з основою три (цифри 0, 1, 2) – трійковою і т.д.
У системах числення з основою меншою десяти використовують десяткові цифри, а для основи більшої десяти добавляють букви латинського алфавіту – А, B, C, D, E, F (табл. 1.1, табл.1.2).
Таблиця 1.1 – Алфавіт систем числення
Основа 
| Система числення | Знаки |
| Двійкова | 0, 1 | |
| Трійкова | 0, 1, 2 | |
| П’ятіркова | 0, 1, 2, 3, 4 | |
| Вісімкова | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Десяткова | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| Шістнадцяткова | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F |
У позиційних системах числення значення кожної цифри визначається її зображенням і позицією в числі. Окремі позиції числа називають розрядами, а номер позиції – номером розряду.
Число розрядів у записі числа називається його розрядністю і збігається з довжиною числа.
У непозиційних системах числення значення кожної цифри не залежить від її позиції.
Найвідомішою непозиційною системою є римська, в якій використовуються сім знаків – І, V, X, L, C, D, M, таким значенням:
| I | V | X | L | C | D | M |
Наприклад: ІІІ – 3, LIX – 59, DLV – 555.
Недоліком непозиційної системи є відсутність нуля та формальних правил запису чисел і відповідно арифметичних дій з ними.
Таблиця 1.2 – Позиційні системи числення
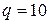
| 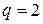
| 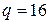
| 
| 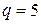
| 
|
| 0 0 0 0 | |||||
| 0 0 0 1 | |||||
| 0 0 1 0 | |||||
| 0 0 1 1 | |||||
| 0 1 0 0 | |||||
| 0 1 0 1 | |||||
| 0 1 1 0 | |||||
| 0 1 1 1 | |||||
| 1 0 0 0 | |||||
| 1 0 0 1 | |||||
| 1 0 1 0 | A | ||||
| 1 0 1 1 | B | ||||
| 1 1 0 0 | C | ||||
| 1 1 0 1 | D | ||||
| 1 1 1 0 | E | ||||
| 1 1 1 1 | F |
Перевагою двійкової системи є:
– простота виконання арифметичних операцій;
– наявність надійних мікроелектронних схем з двома стійкими станами (тригерів), призначених для зберігання значень двійкового розряду – цифр 0 або 1.
Двійкові цифри називають також бітами. Назву БІТ у 1946 році запропонував видатний американський вчений статистик Джон Тюкі.
Система числення повинна забезпечувати:
– можливість представлення будь-якого числа в заданому діапазоні;
– однозначність, стислість запису числа і простоту виконання арифметичних операцій;
– досягнення високої швидкодії машини в процесі оброблення інформації.
Число в позиційній системі можна представити поліномом:
 ,
,
де  – основа системи числення;
– основа системи числення;
 – вага позиції;
– вага позиції;
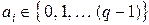 – цифри в позиціях числа;
– цифри в позиціях числа;
 – номери розрядів цілої частини числа;
– номери розрядів цілої частини числа;
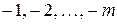 – номери розрядів дробової частини числа.
– номери розрядів дробової частини числа.
Позиційні системи з однаковою основою в кожному розряді називають однорідними.
Приклади запису чисел:
– двійкова система: 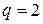 ;
;  ,
,
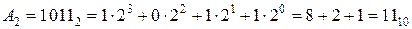 ;
;
– вісімкова система:  ;
; 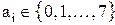 ,
,
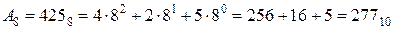 ;
;
– шістнадцяткова система: 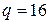 ;
; 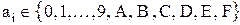 ,
,
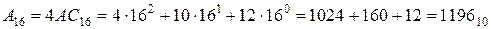 .
.
Дата добавления: 2015-10-19; просмотров: 2649;
