Ряды Тейлора и Лорана
Пьер Альфонс Лоран (1813–1854) — французский математик.
Функция f(z), аналитическая в круге 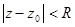 , разлагается в сходящийся к ней степенной ряд по степеням (z – z0).
, разлагается в сходящийся к ней степенной ряд по степеням (z – z0).
Коэффициенты ряда вычисляются по формулам:
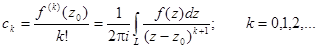
Степенной ряд с коэффициентами такого вида называется рядом Тейлора.
Рассмотрим теперь функцию f(z), аналитическую в кольце 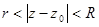 . Эта функция может быть представлена в виде сходящегося ряда:
. Эта функция может быть представлена в виде сходящегося ряда:
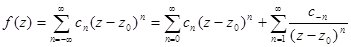
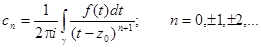
Ряд такого вида называется рядом Лорана. При этом функция f(z) может быть представлена в виде суммы:
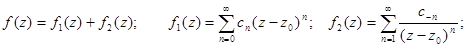
Ряд, определяющий функцию f1(x), называется правильной частью ряда Лорана, а ряд, определяющий функцию f2(x), называется главной частьюряда Лорана.
Если предположить, что r = 0, то можно считать, что функция аналитична в открытом круге 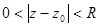 за исключением центральной точки z0. Как правило, в этой точке функция бывает не определена.
за исключением центральной точки z0. Как правило, в этой точке функция бывает не определена.
Тогда точка z0 называется изолированной особой точкойфункции f.
Рассмотрим следующие частные случаи:
1) Функция f(x) имеет вид: 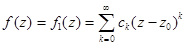 . Т.к. степенной ряд сходится во всех точках внутри круга, то его сумма f1(x) определена и непрерывно дифференцируема во всех точках круга, а, следовательно, и в центре круга z0.
. Т.к. степенной ряд сходится во всех точках внутри круга, то его сумма f1(x) определена и непрерывно дифференцируема во всех точках круга, а, следовательно, и в центре круга z0.
В этом случае говорят, что особенность функции f в точке z0 устранима. Для устранения особой точки достаточно доопределить функцию в центре круга (f(z0) = c0) и функция будет аналитической не только в окрестности центра круга, но и в самом центре.
В этом случае 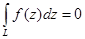 для любого контура L, содержащего точку z0 и принадлежащего к кругу
для любого контура L, содержащего точку z0 и принадлежащего к кругу 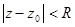 .
.
2) Функция f(x) имеет вид: 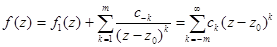 .
.
В этом случае точка z0 называется полюсом функции f(z) порядка (кратности) m.При m = 1 точку z0 называют еще простым полюсом.
Порядок полюса может быть определен по формуле:
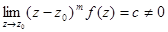
z0 – полюс порядка т.
3) Функция f(z) имеет вид 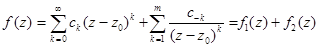 , где в ряду
, где в ряду 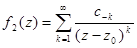 не равно нулю бесконечное количество коэффициентов с-k.
не равно нулю бесконечное количество коэффициентов с-k.
В этом случае говорят, что функция f(z) имеет в точке z0 существенно особую точку.
Определение. Пусть z0 – изолированная особая точка функция f(z), т.е. пусть функция f(z) – аналитическая в некотором круге 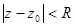 из которого исключена точка z0. Тогда интеграл
из которого исключена точка z0. Тогда интеграл
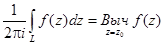
называется вычетом функции f(z) в точке z0, где L – контур в круге 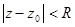 , ориентированный против часовой стрелки и содержащей в себе точку z0.
, ориентированный против часовой стрелки и содержащей в себе точку z0.
Вычет также обозначают иногда 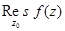 .
.
Если 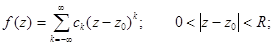 есть ряд Лорана функции f в точке z0, то
есть ряд Лорана функции f в точке z0, то 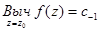 .
.
Таким образом, если известно разложение функции в ряд Лорана, то вычет легко может быть найден в случае любой особой точки.
В частных случаях вычет может быть найден и без разложения в ряд Лорана.
Например, если функция 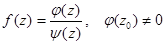 , а
, а 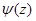 имеет простой нуль при z = z0
имеет простой нуль при z = z0 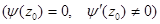 , то z = z0 является простым полюсом функции f(z).
, то z = z0 является простым полюсом функции f(z).
Тогда можно показать, что вычет находится по формуле
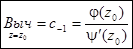
Если z = z0 – полюс порядка m ³ 1, то вычет может быть найден по формуле:
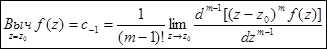
Пример. Найти вычет функции 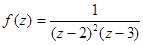 относительно точки z = 2.
относительно точки z = 2.
Эта точка является полюсом второго порядка. Получаем:
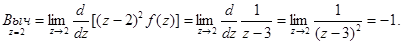
Дата добавления: 2015-10-13; просмотров: 1047;
