Правило Лопиталя. Формула Тейлора
В случае неопределенностей вида 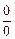 и
и 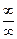 при вычислении пределов часто бывает полезным правило Лопиталя, которое задается следующей теоремой.
при вычислении пределов часто бывает полезным правило Лопиталя, которое задается следующей теоремой.
Теорема 1. Пусть функции f(x) и g(x) удовлетворяют следующим условиям:
1) определены и дифференцируемы на интервале (a; b), за исключением, быть может, точки 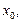 причем
причем 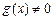 и
и 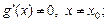
2) 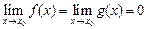 (либо
(либо 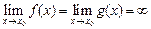 );
);
3) существует предел 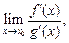 тогда существует предел отношений функций
тогда существует предел отношений функций 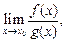 причем
причем
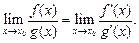 (17.19)
(17.19)
Правило Лопиталя можно использовать последовательно несколько раз.
Аналогичное правило верно в случае 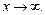
Если при вычислении пределов возникает неопределенность иного вида, то вначале пределы необходимо свести к неопределенности вида 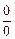 или
или 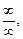 а затем использовать правило Лопиталя.
а затем использовать правило Лопиталя.
В частности, выражения, которые приводят к неопределенностям вида 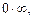
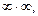 тождественно преобразуют к такому выражению, которое приводят к неопределенности вида
тождественно преобразуют к такому выражению, которое приводят к неопределенности вида 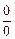 или
или 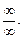
Неопределенности вида 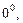
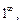
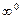 возникают при рассмотрении функции типа
возникают при рассмотрении функции типа 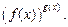 С помощью тождества
С помощью тождества
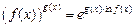 (17.20)
(17.20)
они сводятся к неопределенности вида 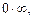 а затем – к
а затем – к 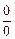 или
или 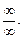
Если функция f(x) имеет в некоторой окрестности точки 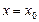 производные до (
производные до ( 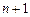 )-го порядка включительно, то при
)-го порядка включительно, то при 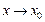 верна формула Тейлора:
верна формула Тейлора:
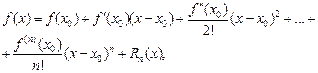 (17.21)
(17.21)
где 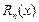 – остаточный член формулы Тейлора.
– остаточный член формулы Тейлора.
Существует несколько форм записи остаточного члена. В частности, в форме Лагранжа:
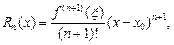
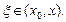
Если в формуле Тейлора 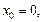 получим частный вид формулы Тейлора – формулу Маклорена:
получим частный вид формулы Тейлора – формулу Маклорена:
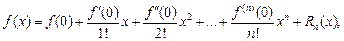
где 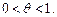
Верны следующие формулы Маклорена:
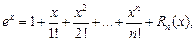 (17.22)
(17.22)
где 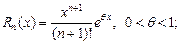
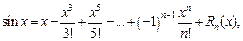
где 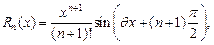
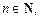
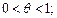
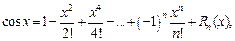 (17.23)
(17.23)
где 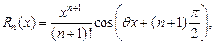
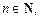
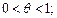
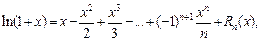 (17.24)
(17.24)
где 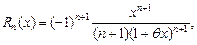
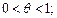
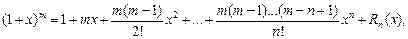
где 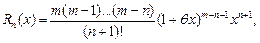
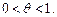
Формулы Маклорена могут быть использованы в приближенных вычислениях. При этом абсолютная погрешность приближения в случае чередования знаков в формуле Маклорена не превосходит абсолютной величины первого отбрасываемого слагаемого.
Пример 1. Вычислить предел функции с помощью правила Лопиталя:
1) 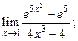 2)
2) 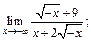 3)
3) 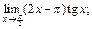
4) 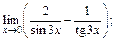 5)
5) 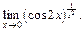
Решение.1) Непосредственное вычисление предела дает неопределенность вида 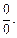 Поскольку условия теоремы 1 выполняются, используем правило Лопиталя. По формуле (17.19) имеем:
Поскольку условия теоремы 1 выполняются, используем правило Лопиталя. По формуле (17.19) имеем:
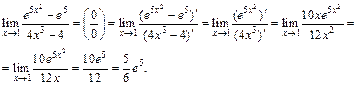
2) Непосредственное вычисление предела дает неопределенность вида 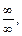 поэтому используем правило Лопиталя:
поэтому используем правило Лопиталя:
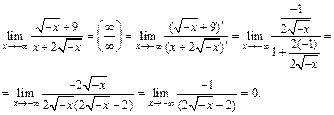
3) Имеем неопределенность вида 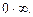 Поэтому, чтобы воспользоваться правилом Лопиталя, преобразуем выражение, стоящее под знаком предела:
Поэтому, чтобы воспользоваться правилом Лопиталя, преобразуем выражение, стоящее под знаком предела:
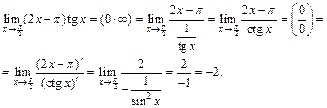
4) Имеем неопределенность вида 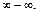 Для того чтобы использовать правило Лопиталя, преобразуем вначале выражение с помощью формул тригонометрии:
Для того чтобы использовать правило Лопиталя, преобразуем вначале выражение с помощью формул тригонометрии:
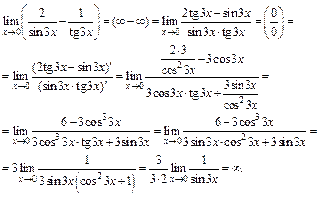
5) Так как приходим к неопределенности вида 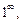 то вначале преобразуем выражение, стоящее под знаком предела:
то вначале преобразуем выражение, стоящее под знаком предела:
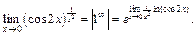
Получили 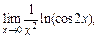 неопределенность вида
неопределенность вида 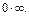 Преобразовав выражение, используем правило Лопиталя:
Преобразовав выражение, используем правило Лопиталя:
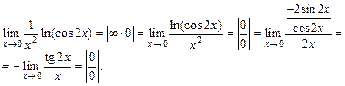
Используем далее эквивалентность бесконечно малых:
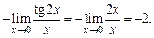
Пример 2. Разложить многочлен 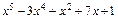 по степени х + 2.
по степени х + 2.
Решение.Используем формулу (17.21). В данном случае 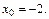 Тогда
Тогда
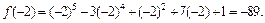
Найдем производные функции:
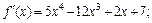
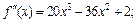
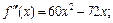
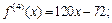
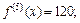
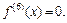
Все производные порядка выше пятого равны нулю. Вычислив значение полученных производных в точке х0 = –2, получаем:
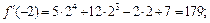
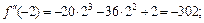
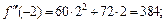
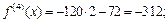
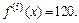
Подставив найденные значения в формулу (17.21), получим:
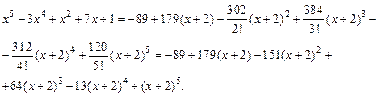
Пример 3. Вычислить предел с помощью формул Маклорена:
1) 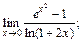 2)
2) 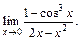
Решение. 1) Используем формулу Маклорена (17.22). Тогда
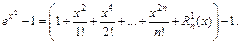
Выражение в правой части равенства эквивалентно величине 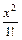 при
при 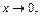 так как остальные слагаемые имеют более высокий порядок малости («быстрее» стремятся к 0), т. е.
так как остальные слагаемые имеют более высокий порядок малости («быстрее» стремятся к 0), т. е.
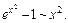
По формуле (17.24) получаем:
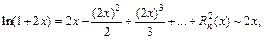 если
если 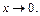
Тогда 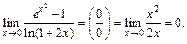
Заметим, что более рациональное решение этого примера возможно с помощью таблицы эквивалентных бесконечно малых, так как использование формул Маклорена выступает здесь как способ доказательства эквивалентностей.
2) Преобразуя выражение под знаком предела и используя формулу (17.23), получим:
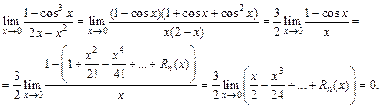
Пример 4. Используя формулу Маклорена, вычислить приближенное значение 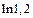 с точностью 0,001.
с точностью 0,001.
Решение. Используем формулу (17.24):
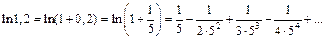
Поскольку знаки чередуются и 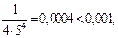 то достаточно взять три слагаемых.
то достаточно взять три слагаемых.
Получаем 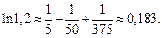
Дата добавления: 2015-09-29; просмотров: 4406;
