Свойства дифференциала

Пусть 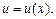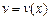– дифференцируемые функции на некотором множестве Тогда:

1)

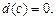
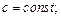
2)

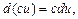
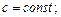
3)

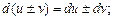
4)

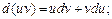
5)

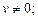
6) 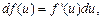где f(u) – сложная функция, дифференцируемая по переменной 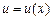(свойство инвариантности дифференциала), т. е.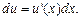

При достаточно малом значении 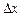приращение функции с большой степенью точности можно заменить дифференциалом функции:

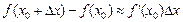
или

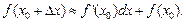(17.11)

Формулу (17.11) используют в приближенных вычислениях.

С геометрической точки зрения дифференциал функции dy равен приращению ординаты касательной к кривой в точке 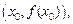когда аргумент получает приращение

Пример 1. Вычислить пр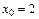и и 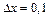значение дифференциала функции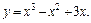

Решение. Дифференциал функции вычислим по формуле (17.10). Найдем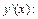

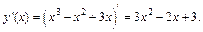
Найдем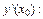

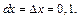
Подставляя найденные значения в формулу (17.10), получим,

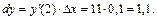
Пример 2. Вычислить дифференциал функции:

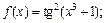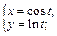1) 2) 3)

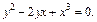
Решение. 1) Найдем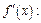

Подставляя полученное выражение в формулу (17.10), получим:

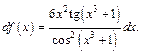
2) Функция задана параметрически. Выразим из первого уравнения системы переменную t через x:

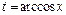
и подставим во второе уравнение:

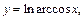
которое продифференцируем как сложную функцию:

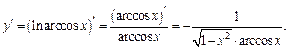
Производную этой функции, заданной параметрически, можно было вычислять также по формуле (17.6).

Используя формулу (17.10) получим:

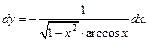
3) Функция задана в неявном виде уравнением

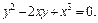
Дифференцируем обе части уравнения, считая, что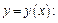

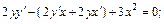
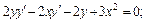
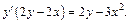
Выразим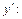

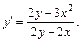
По формуле (17.10), получим:

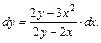
Пример 3. Вычислить приближенно с помощью дифференциала значение выражения:

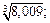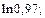1) 2) 3)

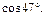
Решение. 1) Воспользуемся формулой (17.11) для функци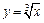и при 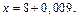Считаем, что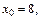

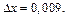
Вычислим

Найдем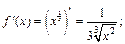

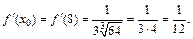
Тогда: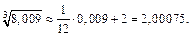

Таким образом,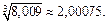

2) Будем находить приближенное значение функции 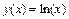в точке 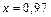по формуле (17.11). Обозначим откуда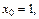

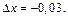
Найдем значение

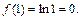
Вычислим производную функции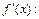

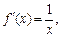откуда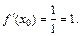

Подставив найденные значения в формулу (17.11), получим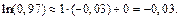

Таким образом, получим ответ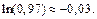

3) Необходимо найти приближенное значение функции в точке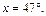

Представим 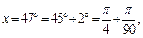откуда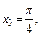

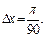
Тогда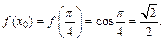

Поскольку 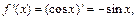то

Тогда по формуле (17.11) получим:

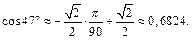
Итак,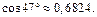

Пример 4.Куб со стороной а = 10 увеличился на 0,05 своего объема. Вычислить приближенно приращение ребра куба.

Решение. Объем куба со стороной a вычисляется по формуле 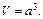Поэтому первоначальный объем куба равен По условию приращение объема куба равно 0,05 всего объема, т. е.

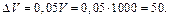
Так как 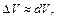то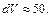

Дифференциал функции вычисляем по формуле (11.9), т. е.

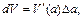откуда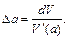

Вычислим значение производной 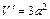для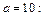

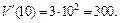
Теперь находим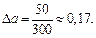

Таким образом, ребро куба увеличилось приблизительно на 0,17.