Функции. Функция f(x) называется дифференцируемой в точке если ее приращение в этой точке может быть представлено в виде

Функция f(x) называется дифференцируемой в точке 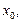если ее приращение 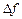в этой точке может быть представлено в виде

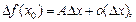(17.7)

где 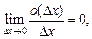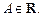(17.8)

Теорема. Для того, чтобы функция f(x) была дифференцируема в точке 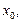необходимо и достаточно, чтобы в точке 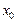существовала производная и в равенстве (17.7) выполнялось условие

Понятие дифференцируемости функции эквивалентно равенству

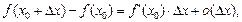(17.9)

где 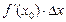– главная часть приращения функции, а для бесконечно малой выполняется (17.8).

Дифференциалом функции f(x) в точке 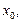называется главная часть 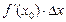приращения функции. Дифференциал обозначается символом 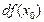и по определению равен

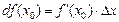
В частности, для функции 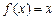получим

Тогда определение дифференциала имеет вид:

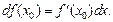(17.10)